围
建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙(利用旧墙需维修)，其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用的旧墙的长度为x(单位：m),修建此矩形场地围墙的总费用为y(单位：元)
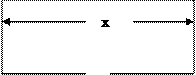
(I)将y表示为x的函数；
(II)试确定x,使修建此矩形场地围墙的总费用最小，并求出最小总费用
在如图所示的几何体中，四边形ABCD是正方形，MA⊥平面ABCD，PD∥MA，E、G、F分别为MB、PB、PC的中点，且AD＝PD＝2MA．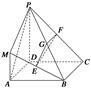
（1）求证：平面EFG∥平面PMA；
（2）求证：平面EFG⊥平面PDC；
（3）求三棱锥P－MAB与四棱锥P－ABCD的体积之比．
有7位歌手（1至7号）参加一场歌唱比赛，由500名大众评委现场投票决定歌手名次．根据年龄将大众评委分为五组，各组的人数如下：
| 组别 |
A |
B |
C |
D |
E |
| 人数 |
50 |
100 |
150 |
150 |
50 |
（1）为了调查评委对7位歌手的支持情况，现用分层抽样方法从各组中抽取若干评委，其中从B组抽取了6人，请将其余各组抽取的人数填入下表．
| 组别 |
A |
B |
C |
D |
E |
| 人数 |
50 |
100 |
150 |
150 |
50 |
| 抽取人数 |
6 |
（2）在（1）中，若A，B两组被抽到的评委中各有2人支持1号歌手，现从这两组被抽到的评委中分别任选1人，求这2人都支持1号歌手的概率．
设数列{an}的前n项和为Sn．已知a1＝1，Sn＋1＝4an＋2．
（1）设bn＝an＋1－2an，证明数列{bn}是等比数列；
（2）求数列{an}的通项公式．
已知
，其中0＜ω＜2．函数
，其图象的一条对称轴为x＝
．
（1）求函数f（x）的表达式及单调递增区间；
（2）在△ABC中，a，b，c分别为角A，B，C的对边，S为其面积，若
，b＝1，S△ABC＝
，求a的值．
平面直角坐标系
中，已知圆
在
轴上截得线段长为
，在
轴上截得线段长为
．
（1）求圆心的轨迹方程；
（2）若点到直线
的距离为
，求圆的方程．