已知二次函数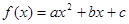 .
.
(Ⅰ)若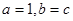 ,且
,且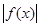 在
在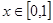 上单调递增,求实数
上单调递增,求实数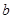 的取值范围;
的取值范围;
(Ⅱ)当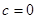 时,有
时,有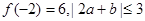 .若对于任意的实数
.若对于任意的实数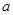 ,存在最大的实数
,存在最大的实数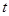 ,使得当
,使得当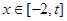 时,
时,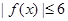 恒成立,试求用
恒成立,试求用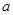 表示
表示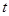 的表达式.
的表达式.
双曲线的中心是原点O,它的虚轴长为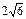 ,右焦点为F(c,0)(c>0),直线
,右焦点为F(c,0)(c>0),直线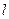 :
: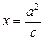 与
与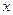 轴交于点A,且| OF |= 3 | OA |.过点F的直线与双曲线交于P、Q两点.
轴交于点A,且| OF |= 3 | OA |.过点F的直线与双曲线交于P、Q两点.
(1)求双曲线的方程;
(2)若 =0,求直线PQ的方程.
=0,求直线PQ的方程.
已知函数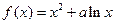 .
.
(1) 当 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值;
(2) 若 在
在 上是单调增函数,求实数
上是单调增函数,求实数 的取值范围.
的取值范围.
已知数列 是等差数列,
是等差数列, 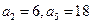 ;数列
;数列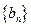 的前n项和是
的前n项和是 ,且
,且 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 求证:数列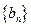 是等比数列;
是等比数列;
(3) 记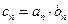 ,求
,求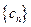 的前n项和
的前n项和 .
.
如图,在四棱锥 中,
中,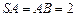 ,
,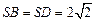 ,底面
,底面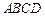 是菱形,且
是菱形,且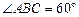 ,
,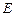 为
为 的中点.
的中点.
(1)求四棱锥 的体积;
的体积;
(2)证明: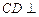 平面
平面 ;
;
(3)侧棱 上是否存在点
上是否存在点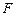 ,使得
,使得 平面
平面 ?并证明你的结论.
?并证明你的结论.
某公司在过去几年内使用某种型号的灯管1000支,该公司对这些灯管的使用寿命(单位:小时)进行了统计,统计结果如下表所示:
| 分组 |
[500,900) |
[900,1100) |
[1100,1300) |
[1300,1500) |
[1500,1700) |
[1700,1900) |
[1900, ) ) |
| 频数 |
48 |
121 |
208 |
223 |
193 |
165 |
42 |
| 频率 |
(1)将各组的频率填入表中;
(2)根据上述统计结果,计算灯管使用寿命不足1500小时的频率;
(3)该公司某办公室新安装了这种型号的灯管2支,若将上述频率作为概率,试求恰有1支灯管的使用寿命不足1500小时的概率.