(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分8分.
(文)对于数列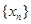 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为 ,公差为
,公差为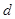 的无穷等差数列
的无穷等差数列 的子数列问题,为此,他取了其中第一项
的子数列问题,为此,他取了其中第一项 ,第三项
,第三项 和第五项
和第五项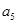 .
.
(1) 若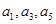 成等比数列,求
成等比数列,求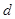 的值;
的值;
(2) 在 ,
, 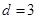 的无穷等差数列
的无穷等差数列 中,是否存在无穷子数列
中,是否存在无穷子数列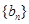 ,使得数列
,使得数列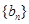 为等比数列?若存在,请给出数列
为等比数列?若存在,请给出数列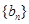 的通项公式并证明;若不存在,说明理由;
的通项公式并证明;若不存在,说明理由;
(3) 他在研究过程中猜想了一个命题:“对于首项为正整数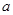 ,公比为正整数
,公比为正整数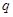 (
(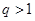 )的无穷等比数 列
)的无穷等比数 列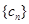 ,总可以找到一个子数列
,总可以找到一个子数列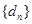 ,使得
,使得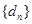 构成等差数列”. 于是,他在数列
构成等差数列”. 于是,他在数列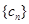 中任取三项
中任取三项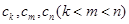 ,由
,由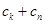 与
与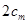 的大小关系去判断该命题是否正确. 他将得到什么结论?
的大小关系去判断该命题是否正确. 他将得到什么结论?
(本小题满分14分)若数列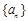 的各项均为正数,
的各项均为正数,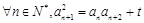 ,
,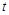 为常数,且
为常数,且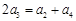 .
.
(1)求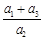 的值;
的值;
(2)证明:数列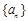 为等差数列;
为等差数列;
(3)若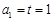 ,对任意给定的k∈N*,是否存在p,r∈N*(k<p<r)使
,对任意给定的k∈N*,是否存在p,r∈N*(k<p<r)使 ,
, ,
, 成等差数列?若存在,用k分别表示一组p和r;若不存在,请说明理由.
成等差数列?若存在,用k分别表示一组p和r;若不存在,请说明理由.
(本小题满分13分)设F1,F2分别是椭圆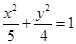 的左右焦点.
的左右焦点.
(1)若P是该椭圆上的一个动点,求 的最大值和最小值.
的最大值和最小值.
(2)是否存在经过点A(5,0)的直线l与椭圆交于不同的两点C,D,使得|F2C|=|F2D|?若存在,求直线l的方程;若不存在,请说明理由.
(本小题满12分)已知函数 .
.
(1)若 =0,判断函数
=0,判断函数 的单调性;
的单调性;
(2)若 时,
时, <0恒成立,求
<0恒成立,求 的取值范围.
的取值范围.
(本小题满分12分)如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, ,
,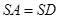 ,
, , N是棱
, N是棱 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: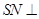 平面
平面 ;
;
(Ⅲ)在棱SC上是否存在一点P,使得平面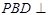 平面
平面 ?若存在,求出
?若存在,求出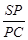 的值;若不存在,说明理由.
的值;若不存在,说明理由.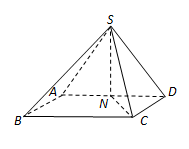
(本小题满分12分)已知函数 ,
, 三个内角
三个内角 的对边分别为
的对边分别为 .
.
(Ⅰ)求 的单调递增区间及对称轴的方程;
的单调递增区间及对称轴的方程;
(Ⅱ)若 ,
, ,
,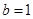 ,求角
,求角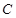 的大小.
的大小.