已知一个圆的圆心为坐标原点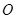 ,半径为
,半径为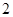 .从这个圆上任意一点
.从这个圆上任意一点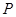 向
向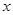 轴作垂线
轴作垂线 ,
,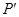 为垂足.
为垂足.
(Ⅰ)求线段 中点
中点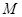 的轨迹方程;
的轨迹方程;
(Ⅱ)已知直线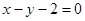 与
与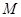 的轨迹相交于
的轨迹相交于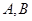 两点,求
两点,求 的面积
的面积
(本小题共14分)

已知双曲线 的离心率为
的离心率为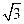 ,右准线方程为
,右准线方程为 。
。
(Ⅰ)求双曲线C的方程;
(Ⅱ)已知直线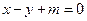 与双曲线C交于不同的两点A,B,且线段AB的中点在圆
与双曲线C交于不同的两点A,B,且线段AB的中点在圆 上,求m的值.
上,求m的值.
(直线y=kx+b与曲线 交于A、B两点,记△AOB的面积为S(O是坐标原点).
交于A、B两点,记△AOB的面积为S(O是坐标原点).
(1)求曲线的离心率;
(2)求在k=0,0<b<1的条件下,S的最大值;
(3)当|AB|=2,S=1时,求直线AB的方程.
如图,已知抛物线的方程为 ,
,
过点M(0,m)且倾斜角为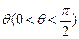 的直线交抛物线于
的直线交抛物线于
A(x1,y1),B(x2,y2)两点,且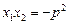
(1)求m的值
(2)(文)若点M分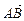 所成的比为
所成的比为 ,求直线AB的方程
,求直线AB的方程
(理)若点M分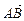 所成的比为
所成的比为 ,求
,求 关于
关于 的函数关系式。
的函数关系式。
已知以向量v=(1,  )为方向向量的直线l过点(0,
)为方向向量的直线l过点(0,  ),抛物线C:
),抛物线C: (p>0)的顶点关于直线l的对称点在该抛物线上.
(p>0)的顶点关于直线l的对称点在该抛物线上.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若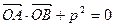 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程.
已知A,B是抛物线 上的两个动点,
上的两个动点,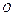 为坐标原点,非零向量
为坐标原点,非零向量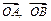 满足
满足 .
.
(Ⅰ)求证:直线 经过一定点;
经过一定点;
(Ⅱ)当 的中点到直线
的中点到直线 的距离的最小值为
的距离的最小值为 时,求
时,求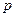 的值.
的值.