函数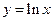 关于直线
关于直线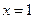 对称的函数为
对称的函数为 ,又函数
,又函数 的导函数为
的导函数为 ,记
,记 .
.
(Ⅰ)设曲线 在点
在点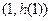 处的切线为
处的切线为 ,
,  与圆
与圆 相切,求
相切,求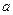 的值;
的值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)求函数 在[0,1]上的最大值.
在[0,1]上的最大值.
函数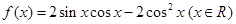 .
.
(1)求函数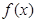 的最小正周期;
的最小正周期;
(2)当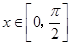 时,求函数
时,求函数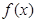 的取值范围.
的取值范围.
已知向量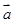 =(1,2),
=(1,2),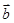 =(2,-2).
=(2,-2).
(1)设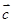 =4
=4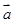 +
+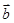 ,求(
,求(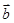 ·
·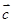 )
)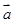 ;
;
(2)若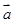 +λ
+λ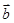 与
与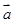 垂直,求λ的值;
垂直,求λ的值;
已知函数 .
.
(I)求函数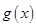 的单调区间;
的单调区间;
(II)若函数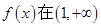 上是减函数,求实数
上是减函数,求实数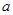 的最小值;
的最小值;
(III)若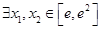 ,使
,使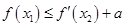 成立,求实数
成立,求实数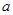 的取值范围.
的取值范围.
如图,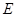 是以
是以 为直径的半圆上异于
为直径的半圆上异于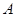 、
、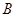 的点,矩形
的点,矩形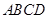 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且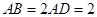 .
.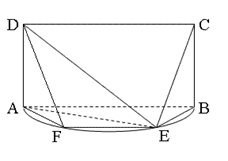
(Ⅰ)求证: ;
;
(Ⅱ)设平面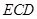 与半圆弧的另一个交点为
与半圆弧的另一个交点为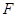 .
.
①试证: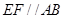 ;
;
②若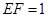 ,求三棱锥
,求三棱锥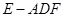 的体积.
的体积.
如图,抛物线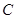 的顶点为坐标原点
的顶点为坐标原点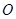 ,焦点
,焦点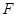 在
在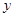 轴上,准线
轴上,准线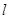 与圆
与圆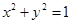 相切.
相切.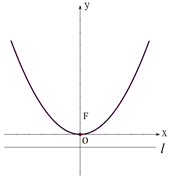
(Ⅰ)求抛物线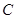 的方程;
的方程;
(Ⅱ)已知直线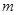 和抛物线
和抛物线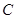 交于点
交于点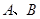 ,命题P:“若直线
,命题P:“若直线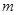 过定点
过定点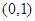 ,则
,则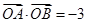 ”,请判断命题P的真假,并证明。
”,请判断命题P的真假,并证明。