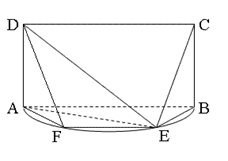
如图,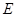 是以
是以 为直径的半圆上异于
为直径的半圆上异于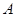 、
、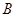 的点,矩形
的点,矩形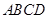 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且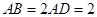 .
.
(Ⅰ)求证: ;
;
(Ⅱ)设平面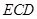 与半圆弧的另一个交点为
与半圆弧的另一个交点为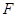 .
.
①试证: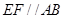 ;
;
②若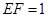 ,求三棱锥
,求三棱锥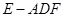 的体积.
的体积.
(本小题满分14分)
设函数f(x)=x3-x2+bx+c,其中a>0,曲线y=f(x)在点P(0,f(0))处的切线方程为
y=1.
(1)确定b,c的值;
(2)设曲线y=f(x)在点(x1,f(x1))及(x2,f(x2))处的切线都过点(0,2).
证明:当x1≠x2时,f ′(x1)≠f ′(x2);
(3)若过点(0,2)可作曲线y=f(x)的三条不同切线,求a的取值范围.
(本小题满分13分)
设数列{an}满足a1=t,a2=t2,前n项和为Sn,且Sn+2-(t+1)Sn+1+tSn=0(n∈N*).
(1)证明数列{an}为等比数列,并求{an}的通项公式;
(2)当<t<2时,比较2n+2-n与tn+t-n的大小;
(3)若<t<2,bn=,求证:++…+<2n- .
.
(本小题满分12分)
某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=x2+10x(万元);当年产量不小于80千件时,C(x)=51x+-1450(万元).通过市场分析,若每件售价为500元时,该厂当年生产的该产品能全部销售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一产品的生产中所获利润最大,最大利润是多少?
(本小题满分12分)
已知数列{an}的前n项和Sn=2n2-2n,数列{bn}的前n项和Tn=3-bn.
①求数列{an}和{bn}的通项公式;
②设cn=an·bn,求数列{cn}的前n项和Rn的表达式.
(本小题满分12分)
已知△ABC的内角A,B,C所对的边分别为a,b,c,且a=2,cos2B=- .
.
(1)若b=4,求sinA的值;
(2)若△ABC的面积S△ABC=4,求b,c的值.