(本小题满分12分)
已知数列{an}的前n项和Sn=2n2-2n,数列{bn}的前n项和Tn=3-bn.
①求数列{an}和{bn}的通项公式;
②设cn=an·bn,求数列{cn}的前n项和Rn的表达式.
设数列
的前
项和为Sn,满足
,且
,
,
成等差数列.
(1)求
的值;
(2)求数列
的通项公式;
(3)证明:对一切正整数
,有
.
如图所示,在四棱锥
中,底面
为矩形,
平面
,点
在线段
上,
平面
.
(1)证明:
平面
;
(2)若
,
,求二面角
的正切值.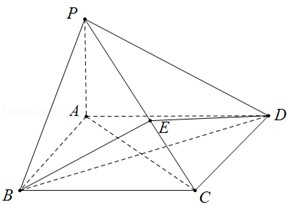
某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中
的值;
(2)从成绩不低于80分的学生中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为
,求
的数学期望.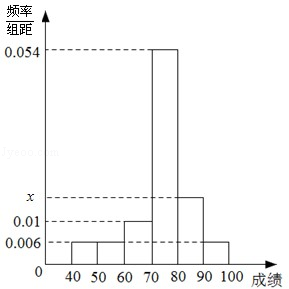
已知函数
(其中
)的最小正周期为
.
(1)求
的值;
(2)设
,求
的值.
在平面直角坐标系
中,已知椭圆
.如图所示,斜率为
且不过原点的直线
交椭圆
于
,
两点,线段
的中点为
,射线
交椭圆
于点
,交直线
于点
.
(1)求
的最小值;
(2)若
(i)求证:直线
过定点;
(ii)试问点
能否关于
轴对称?若能,求出此时
的外接圆方程;若不能,请说明理由.