直线AB经过⊙O上的点C,并且OA=OB,CA=CB.⊙O交直线OB于E,D,连接EC,CD.
(Ⅰ)求证:直线AB是⊙O的切线;
(2)若tan∠CED=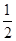 ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.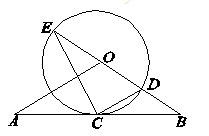
(本小题满分13分)
已知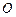 为平面直角坐标系的原点,过点
为平面直角坐标系的原点,过点 的直线
的直线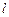 与圆
与圆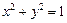 交于
交于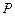 ,
, 两点.
两点.
(I)若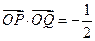 ,求直线
,求直线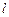 的方程;
的方程;
(Ⅱ)若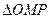 与
与 的面积相等,求直线
的面积相等,求直线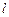 的斜率.
的斜率.
(本小题满分13分)
已知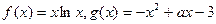 .
.
(I)求函数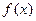 在
在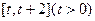 上的最小值;
上的最小值;
(II)对一切 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分13分)
如图,四边形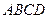 为正方形,
为正方形,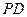 ⊥平面
⊥平面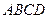 ,
,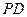 ∥
∥ ,
, =
= =
= .
.
(I)证明:平面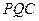 ⊥平面
⊥平面 ;
;
(II)求二面角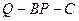 的余弦值.
的余弦值.
(本小题满分13分)
在 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足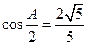 ,
, .
.
(I)求 的面积;
的面积;
(II) 若 ,求
,求 的值.
的值.
(本小题满分13分)
椭圆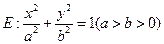 的离心率为
的离心率为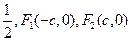 分别是左、右焦点,过F1的直线与圆
分别是左、右焦点,过F1的直线与圆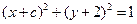 相切,且与椭圆E交于A、B两点。
相切,且与椭圆E交于A、B两点。
(1)当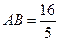 时,求椭圆E的方程;
时,求椭圆E的方程;
(2)求弦AB中点的轨迹方程。