如图,四棱锥 中,
中,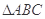 是正三角形,四边形
是正三角形,四边形 是矩形,且平面
是矩形,且平面 平面
平面 ,
,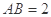 ,
, .
.
(1)若点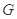 是
是 的中点,求证:
的中点,求证: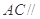 平面
平面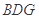
(2)若 是线段
是线段 的中点,求三棱锥
的中点,求三棱锥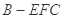 的体积.
的体积.
(本小题满分15分)已知椭圆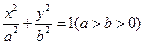 的离心率为
的离心率为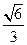 ,过
,过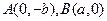 的直线与原点的距离为
的直线与原点的距离为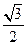
(1)求椭圆的方程;
(2)已知定点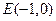 ,直线
,直线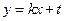 与椭圆交于不同两点C,D,试问:对任意的
与椭圆交于不同两点C,D,试问:对任意的 ,是否都存在实数
,是否都存在实数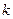 ,使得以线段CD为直径的圆过点E?证明你的结论
,使得以线段CD为直径的圆过点E?证明你的结论
(本小题满分14分)
等差数列 的前
的前 项和为
项和为 ,且
,且
(1)求 的通项公式
的通项公式 ;
;
(2)若数列 满足
满足 且
且 求
求 的前
的前 项和
项和
本小题满分14分)
经市场调查,某旅游城市在过去的一个月内(以30天计),日旅游人数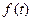 (万人)与时间
(万人)与时间 (天)的函数关系近似满足
(天)的函数关系近似满足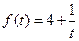 ,日人均消费
,日人均消费 (元)与时间
(元)与时间 (天)的函数关系近似满足
(天)的函数关系近似满足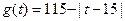
(1)求该城市的旅游日收益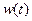 (万元)与时间
(万元)与时间 的函数关系式;
的函数关系式;
(2)求该城市旅游日收益的最小值(万元)
(本小题满分14分)
已知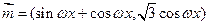 ,
,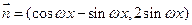 ,其中
,其中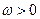 ,若函数
,若函数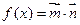 ,且函数
,且函数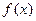 的图象与直线
的图象与直线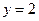 相邻两公共点间的距离为
相邻两公共点间的距离为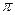
(1)求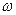 的值;
的值;
(2)在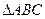 中,
中,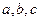 分别是角
分别是角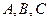 的对边,且
的对边,且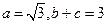 ,
,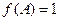 ,求
,求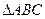 的面积.
的面积.
(本小题满分10分)选修4-5:不等式选讲
已知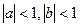 ,求证:
,求证: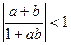 .
.