（本小题满分14分）
设函数f(x)＝x3－x2＋bx＋c，其中a>0，曲线y＝f(x)在点P(0，f(0))处的切线方程为
y＝1.
(1)确定b，c的值；
(2)设曲线y＝f(x)在点(x1，f(x1))及(x2，f(x2))处的切线都过点(0,2)．
证明：当x1≠x2时，f ′(x1)≠f ′(x2)；
(3)若过点(0,2)可作曲线y＝f(x)的三条不同切线，求a的取值范围．
在△ABC中，∠C＝90°，M是BC的中点．若sin∠BAM＝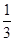
，则sin∠BAC＝________.
如图，四棱柱ABCD—A1B1C1D1中，侧棱A1A⊥底面ABCD，AB∥DC，AB⊥AD，AD＝CD＝1，AA1＝AB＝2，E为棱AA1的中点．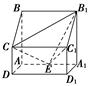
(1)证明B1C1⊥CE；
(2)求二面角B1CEC1的正弦值；
(3)设点M在线段C1E上，且直线AM与平面ADD1A1所成角的正弦值为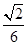
，求线段AM的长．
如图所示，PA⊥平面ABC，点C在以AB为直径的⊙O上，∠CBA＝30°，PA＝AB＝2，点E为线段PB的中点，点M在弧AB上，且OM∥AC.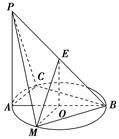
(1)求证：平面MOE∥平面PAC.
(2)求证：平面PAC⊥平面PCB.
(3)设二面角M—BP—C的大小为θ，求cos θ的值．
已知数列{an}的前n项和为Sn，且Sn＝2an－2，数列{bn}满足b1＝1，且bn＋1＝bn＋2.
(1)求数列{an}，{bn}的通项公式；
(2)设c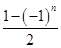n＝
an－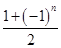
bn，求数列{cn}的前2n项和T2n.
如图，三棱柱ABC—A1B1C1的侧面AA1B1B为正方形，侧面BB1C1C为菱形，∠CBB1＝60°，AB⊥B1C.
(1)求证：平面AA1B1B⊥平面BB1C1C；
(2)若AB＝2，求三棱柱ABC—A1B1C1的体积．