(本小题满分13分)
设数列{an}满足a1=t,a2=t2,前n项和为Sn,且Sn+2-(t+1)Sn+1+tSn=0(n∈N*).
(1)证明数列{an}为等比数列,并求{an}的通项公式;
(2)当<t<2时,比较2n+2-n与tn+t-n的大小;
(3)若<t<2,bn=,求证:++…+<2n- .
.
在△ABC中,角A,B,C的对边分别为 ,且
,且 .
.
(Ⅰ)求sin2A;(Ⅱ)若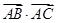 =4,且
=4,且 ,求
,求 .
.
已知抛物线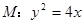 ,圆
,圆 ,过点
,过点 作直线
作直线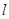 ,自上而下依次与上述两曲线交于点
,自上而下依次与上述两曲线交于点 (如图所示),
(如图所示), .
.
(Ⅰ)求 ;
;
(Ⅱ)作 关于
关于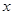 轴的对称点
轴的对称点 ,求证:
,求证: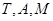 三点共线;
三点共线;
(Ⅲ)作 关于
关于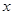 轴的对称点
轴的对称点 ,求
,求 到直线
到直线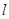 的距离的最大值.
的距离的最大值.
在数列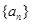 中,
中, ,当
,当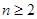 时,满足
时,满足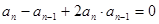 .
.
(Ⅰ)求证:数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)令 ,数列
,数列 的前
的前 项和为
项和为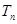 ,求使得
,求使得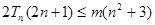 对所有
对所有 都成立的实数
都成立的实数 的取值范围.
的取值范围.
如图,四棱锥 中,面
中,面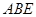
 面
面 ,侧面
,侧面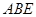 是等腰直角三角形,
是等腰直角三角形, ,且
,且 ∥
∥ ,
,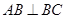 ,
, .
.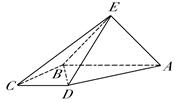
(Ⅰ)求证: ;
;
(Ⅱ)求直线 与面
与面 的所成角的正弦值.
的所成角的正弦值.
已知不等式组 的解集是
的解集是 ,且存在
,且存在 ,使得不等式
,使得不等式 成立.
成立.
(Ⅰ)求集合 ;
;
(Ⅱ)求实数 的取值范围.
的取值范围.