已知抛物线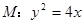 ,圆
,圆 ,过点
,过点 作直线
作直线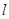 ,自上而下依次与上述两曲线交于点
,自上而下依次与上述两曲线交于点 (如图所示),
(如图所示), .
.
(Ⅰ)求 ;
;
(Ⅱ)作 关于
关于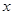 轴的对称点
轴的对称点 ,求证:
,求证: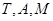 三点共线;
三点共线;
(Ⅲ)作 关于
关于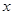 轴的对称点
轴的对称点 ,求
,求 到直线
到直线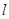 的距离的最大值.
的距离的最大值.
如图,三棱柱ABC-A1B1C1的所有棱长都是2,又AA1⊥平面ABC,D,E分别是AC,CC1的中点.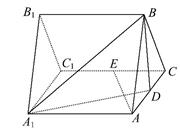
(1)求证:AE⊥平面A1BD.
(2)求二面角D-BA1-A的余弦值.
(3)求点B1到平面A1BD的距离.
已知单调递增的等比数列 满足:
满足: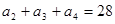 ,且
,且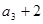 是
是 ,
, 的等差中项。
的等差中项。
(1)求数列 的通项公式;
的通项公式;
(2)若 ,
,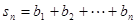 ,求
,求 成立的正整数
成立的正整数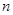 的最小值.
的最小值.
已知函数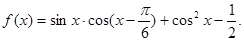
(1)求函数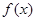 的单调递增区间和对称中心。
的单调递增区间和对称中心。
(2)在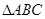 中,角
中,角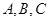 的对边分别为
的对边分别为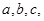 ,若
,若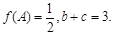 求
求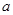 的最小值.
的最小值.
已知函数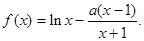
(1)若函数 上为单调增函数,求a的取值范围;
上为单调增函数,求a的取值范围;
(2)设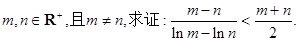
已知椭圆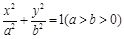 的右焦点为
的右焦点为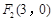 ,离心率为
,离心率为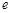 .
.
(Ⅰ)若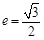 ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)设直线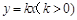 与椭圆相交于
与椭圆相交于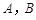 两点,若
两点,若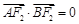 ,且
,且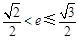 ,求
,求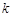 的最小值.
的最小值.