(本小题满分12分)在如图所示的空间几何体中,平面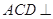 平面
平面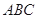 ,
,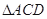 与
与 是边长为
是边长为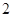 的等边三角形,
的等边三角形,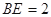 ,
, 和平面
和平面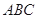 所成的角为
所成的角为 ,且点
,且点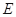 在平面
在平面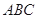 上的射影落在
上的射影落在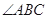 的平分线上.
的平分线上.
(Ⅰ)求证: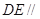 平面
平面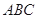 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
(本小题满分12分)甲、乙两人参加某种选拔测试.在备选的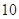 道题中,甲答对其中每道题的概率都是
道题中,甲答对其中每道题的概率都是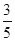 ,乙能答对其中的
,乙能答对其中的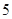 道题.规定每次考试都从备选的
道题.规定每次考试都从备选的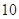 道题中随机抽出
道题中随机抽出 道题进行测试,答对一题加
道题进行测试,答对一题加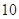 分,答错一题(不答视为答错)减
分,答错一题(不答视为答错)减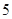 分,至少得
分,至少得 分才能入选.
分才能入选.
(1)求乙得分的分布列和数学期望;
(2)求甲、乙两人中至少有一人入选的概率.
(本小题满分12分)公差不为零的等差数列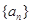 中,
中, 且
且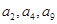 成等比数列。
成等比数列。
(1)求数列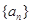 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的通项公式
的通项公式
附加题:本题满分10分.已知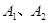 是平面内两个定点,且
是平面内两个定点,且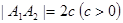 ,若动点
,若动点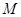 与
与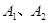 连线的斜率之积等于常数
连线的斜率之积等于常数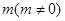 ,求点
,求点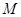 的轨迹方程,并讨论轨迹形状与
的轨迹方程,并讨论轨迹形状与 值的关系.
值的关系.
(本小题满分14分) 已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在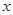 轴上,离心率等于
轴上,离心率等于 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线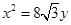 的焦点.
的焦点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)点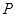
 ,
,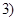 ,
, 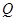
 ,
, 在椭圆上,
在椭圆上,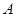 、
、 是椭圆上位于直线
是椭圆上位于直线 两侧的动点.
两侧的动点.
①若直线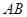 的斜率为
的斜率为 ,求四边形
,求四边形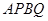 面积的最大值;
面积的最大值;
②当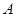 、
、 运动时,满足于
运动时,满足于 ,试问直线
,试问直线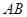 的斜率是否为定值?若是,请求出定值,若不是,请说明理由.
的斜率是否为定值?若是,请求出定值,若不是,请说明理由.