（本小题满分12分）某学校研究性学习小组对该校高三学生视力情况进行调查，在高三的全体
1000名学生中随机抽取了若干名学生的体检表，并得到如下直方图：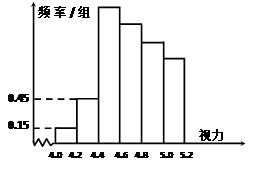
（Ⅰ）若直方图中前三组的频率成等比数列，后四组的频率成等差数列，试估计全年级视力在5.0以下的
人数；
（Ⅱ）学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有
关系，对年级名次在1~50名和951~1000名的学生进行了调查，得到如下数据：
根据表中的数据，能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
附：
| P(K2≥k) |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
| k |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
在平面直角坐标系xOy中，点B与点A（-1,1）关于原点O对称，P是动点，且直线AP与BP的斜率之积等于
.(Ⅰ)求动点P的轨迹方程；
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N，问：是否存在点P使得△PAB与△PMN的面积相等？若存在，求出点P的坐标；若不存在，说明理由。
设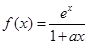
，其中
为正实数
（Ⅰ）当
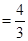时，求
的极值点；
（Ⅱ）若为
上的单调函数，求的取值范围。
已知函数
的图象与
在原点相切，且函数的极小值为
，（1）求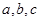
的值；（2）求函数的递减区间．
设命题
：函数
在
上递增；命题
：函数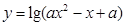
的定义域为R．若或为真，且为假，求
的取值范围．
的三个顶点为
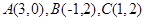，求：
（Ⅰ）BC边上的中线AD所在直线的方程；（Ⅱ）的外接圆方程。