甲、乙、丙三台机床各自独立的加工同一种零件,已知甲、乙、丙三台机床加工的零件是一等品的概率分别为0.7、0.6、0.8,乙、丙两台机床加工的零件数相等,甲机床加工的零件数是乙机床加工的零件数的二倍.
(1)从甲、乙、丙加工的零件中各取一件检验,求至少有一件一等品的概率;
(2)将三台机床加工的零件混合到一起,从中任意的抽取一件检验,求它是一等品的概率;
(3)将三台机床加工的零件混合到一起,从中任意的抽取4件检验,求一等品的个数不少于3个的概率。
(本小题满分12分)(文)设函数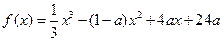 ,其中常数a>1
,其中常数a>1
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若当x≥0时,f(x)>0恒成立,求a的取值范围。2
21、(理)已知 是函数
是函数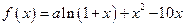 的一个极值点。
的一个极值点。
(Ⅰ)求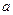 的值;
的值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(本小题满分12分)如图,直三棱柱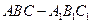 中,AB=1,
中,AB=1, ,∠ABC=60
,∠ABC=60 .
.
(Ⅰ)证明: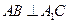 ;
;
(Ⅱ)求二面角A— —B的大小。
—B的大小。
(理)数列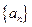 的前
的前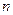 项和记为
项和记为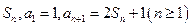
(Ⅰ)求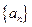 的通项公式;
的通项公式;
(Ⅱ)等差数列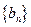 的各项为正,其前
的各项为正,其前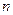 项和为
项和为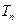 ,且
,且 ,又
,又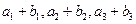 成等比数列,求
成等比数列,求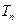
(本小题满分12分)(文)甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束。假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立。已知前2局中,甲、乙各胜1局。
(Ⅰ)求再赛2局结束这次比赛的概率;
(Ⅱ)(文)求甲获得这次比赛胜利的概率。
(理)设进入某商场的每一位顾客购买甲种商品的概率为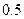 ,购买乙种商品的概率为
,购买乙种商品的概率为 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记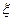 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求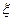 的分布列及期望。
的分布列及期望。