设椭圆M：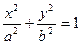
(a＞b＞0)的离心率为
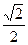，长轴长为
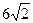，设过右焦点F倾
斜角为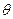
的直线交椭圆M于A，B两点。
（Ⅰ）求椭圆M的方程；
（2）设过右焦点F且与直线AB垂直的直线交椭圆M于C，D，求|AB| + |CD|的最小
值。
已知二次函数的图象如图所示．
（1）写出函数的零点；
（2）写出该函数的解析式．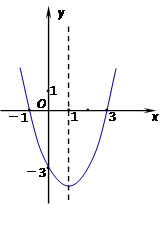
已知U＝R，A＝｛x|－1≤x≤3｝，B＝｛x|x－a＞0｝．
(1)若AÍB，求实数a的取值范围；
(2) 若A∩B≠Æ，求实数a的取值范围．
计算：2log32－log3
＋log38－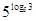
（本小题满分14分）
已知函数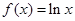
，
．
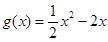（1）设
（其中
是
的导函数），求
的最大值；
（2）证明: 当
时，求证：
；
（3）设
,当
时,不等式
恒成立,求
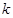的最大值．
（本小题满分12分）
已知椭圆C：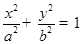
(a>b>0)的离心率为
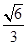，短轴一个端点到右焦点的距离为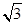
（1）求椭圆C的方程；
（2）设直线l与椭圆C交于A、B两点，坐标原点O到直线l的距离为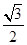
，求△AOB面积的最大值．