某市十所重点中学进行高三联考,共有5000名考生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表:
(1)根据上面的频率分布表,求①,②,③,④处的数值;
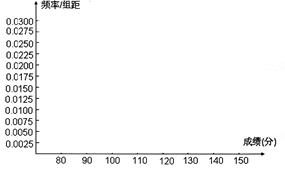
(2)根据上面的频率分布表,在所给的坐标系中画出在区间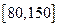 上的频率分布直方图;
上的频率分布直方图;
(3)如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率,那么从总体中任意抽取3个个体,成绩落在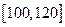 中的个体数为
中的个体数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
| 分组 |
频数 |
频率 |
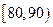 |
① |
② |
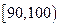 |
|
0.050 |
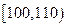 |
|
0.200 |
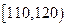 |
36 |
0.300 |
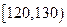 |
|
0.275 |
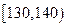 |
12 |
③ |
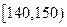 |
|
0.050 |
| 合计 |
④ |
|
(本小题满分16分)
已知函数 =
=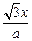 +
+ ,a≠0且a≠1.
,a≠0且a≠1.
(1)试就实数a的不同取值,写出该函数的单调增区间;
(2)已知当x>0时,函数在(0, )上单调递减,在(
)上单调递减,在( ,
, 上单调递增,求a的值并写出函数的解析式;
上单调递增,求a的值并写出函数的解析式;
(3)记(2)中的函数图象为曲线C,试问是否存在经过原点的直线l,使得l为曲线C的对称轴?若存在,求出直线l的方程;若不存在,请说明理由.
(本小题满分16分)
已知F是椭圆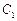 :
: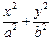 =1的右焦点,点P是椭圆
=1的右焦点,点P是椭圆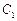 上的动点,点Q是圆
上的动点,点Q是圆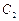 :
: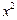 +
+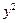 =
=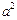 上的动点.
上的动点.
(1)试判断以PF为直径的圆与圆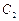 的位置关系;
的位置关系;
(2)在x轴上能否找到一定点M,使得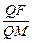 =e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
=e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
.(本小题满分14分)
如图,在边长为10的正三角形纸片ABC的边AB,AC上分别取D,E两点,使沿线段DE折叠三角形纸片后,顶点A正好落在边BC上(设为P),在这种情况下,求AD的最小值.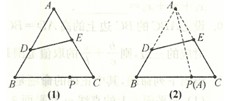
(本小题满分14分)
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=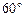 ,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.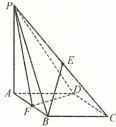
(1)求证:BE∥平面PDF;
(2)求证:平面PDF⊥平面PAB;
(3)求三棱锥P-DEF的体积.
(本小题满分14分)
已知点A(3,0),B(0,3),C(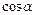 ,
,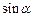 ),
),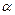 ∈
∈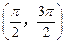 .
.
(1)若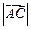 =
=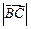 ,求角
,求角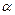 的值;
的值;
(2)若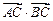 =-1,求
=-1,求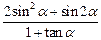 的值.
的值.