设曲线y=x2+x+1-ln x在x=1处的切线为l,数列{an}中,a1=1,且点(an,an+1)在切线l上.
(1)求证:数列{1+an}是等比数列,并求an;
(2)求数列{an}的前n项和Sn.
(本小题满分14分)省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数f(x)与时刻x(时)的关系为f(x)=+2a+,x∈,其中a是与气象有关的参数,且a∈],若取每天f(x)的最大值为当天的综合放射性污染指数,并记作M(a).
(1) 令t=,x∈,求t的取值范围;
(2) 省政府规定,每天的综合放射性污染指数不得超过2,试问:目前市中心的综合放射性污染指数是否超标?
(本小题满分14分)已知在直四棱柱ABCDA1B1C1D1中,底面ABCD为直角梯形,且满足AD⊥AB,BC∥AD,AD=16,AB=8,BB1=8,E,F分别是线段A1A,BC上的点.
(1) 若A1E=5,BF=10,求证:BE∥平面A1FD.
(2) 若BD⊥A1F,求三棱锥A1AB1F的体积.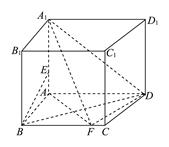
(本小题满分14分)已知函数f(x)=sin2x+sinxcosx-(x∈R).
(1) 若x∈,求f(x)的最大值;
(2) 在△ABC中,若A<B,f(A)=f(B)=,求的值.
已知椭圆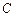 :
: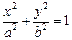 (
(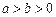 )的离心率
)的离心率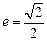 ,左、右焦点分别为
,左、右焦点分别为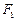 、
、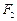 ,点
,点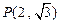 满足:
满足: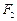 在线段
在线段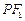 的中垂线上.
的中垂线上.
(1)求椭圆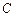 的方程;
的方程;
(2)若斜率为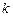 (
(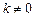 )的直线
)的直线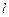 与
与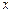 轴、椭圆
轴、椭圆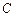 顺次相交于点
顺次相交于点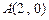 、
、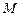 、
、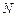 ,且
,且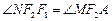 ,求
,求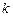 的取值范围.
的取值范围.
已知函数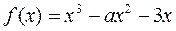 .
.
(1)若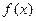 在
在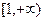 上是增函数, 求实数a的取值范围.
上是增函数, 求实数a的取值范围.
(2)若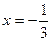 是
是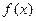 的极大值点,求
的极大值点,求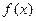 在
在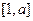 上的最大值;
上的最大值;
(3)在(2)的条件下,是否存在实数b,使得函数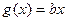 的图像与函数
的图像与函数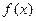 的图像恰有3个交点,若存在,求出b的取值范围,若不存在,说明理由.
的图像恰有3个交点,若存在,求出b的取值范围,若不存在,说明理由.