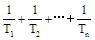现有甲乙两个团队之间进行某种比赛,与身高有很大的关系(假定忽略其它因素),为了预知比赛结果,在甲乙两个团队中各随机抽调出8人,测量身高并绘出茎叶图如图。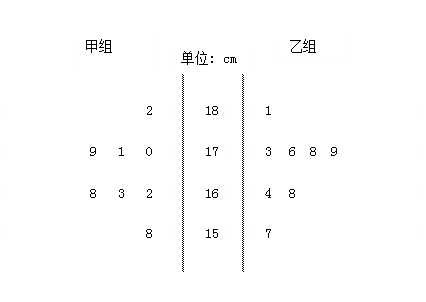
(1)请你根据茎叶图判断一下如果是跨越障碍物比赛,哪个团队胜出的可能性大一些?说明你的理由。
(2)如果是进行队形整齐性比赛(身高相对要整齐),哪个团队胜出的可能性又大一些?说明你的理由。
(3)从甲团队的这抽出的8人中的身高低于170cm的队员中再抽取两名进行某种灵巧性训练,则身高为158cm的那位队员被选中的概率是多少?
(本小题满分12分)
在数列 中,
中,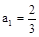 ,若函数
,若函数 在点
在点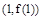 处切线过点(
处切线过点( )
)
(1)求证:数列 为等比数列;
为等比数列;
(2)求数列 的通项公式和前n项和公式
的通项公式和前n项和公式 .
.
(本小题满分12分)
若向量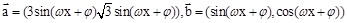 ,其中
,其中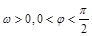 ,设函数
,设函数 ,其周期为
,其周期为 ,且
,且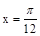 是它的一条对称轴。
是它的一条对称轴。
(1)求 的解析式;
的解析式;
(2)当 时,不等式
时,不等式 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)设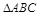 的内角
的内角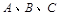 的对边分别为a、b、c,若c=
的对边分别为a、b、c,若c=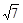 ,
, 求a,b的值
求a,b的值
(本小题满分14分)已知函数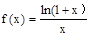
(1)确定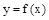 在(0,+
在(0,+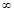 )上的单调性;
)上的单调性;
(2)设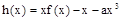 在(0,2)上有极值,求a的取值范围.
在(0,2)上有极值,求a的取值范围.
(本小题满分12分)已知数列{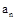 }的前n项和为
}的前n项和为 ,数列
,数列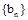 的前n项和为
的前n项和为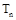 ,
,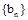 为等差数列且各项均为正数,
为等差数列且各项均为正数,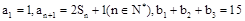
(1)求数列{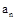 }的通项公式;
}的通项公式;
(2)若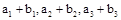 成等比数列,求
成等比数列,求