(本小题满分12分)如图，在三棱锥A－BCD中，侧面ABD、 ACD是全等的直角三角形，AD是公共的斜边，且AD＝
，BD＝CD＝1，另一个侧面是正三角形.
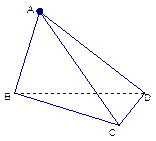
（1） 求证：AD^BC;
（2） 求二面角B－AC－D的大小;
（3） 在直线AC上是否存在一点E，使ED与面BCD成30°角？若存在，确定E的位置；若不存在，说明理由
已知等比数列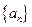
中，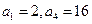
。
（1）求数列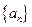的通项公式；
（2）设等差数列
中，
，求数列的前
项和
。
双曲线C：－y2＝1，设过A(－3，0)的直线l的方向向量e＝(1，k)．
(1)当直线l与双曲线C的一条渐近线m平行时，求直线l的方程及l与m的距离；
(2)证明：当k＞时，在双曲线C的右支上不存在点Q，使之到达直线l的距离为.
已知双曲线的中心在原点，焦点F1、F2在坐标轴上，离心率为，且过点(4，－)．
(1)求双曲线方程；
(2)若点M(3，m)在双曲线上，求证：MF1⊥MF2；
(3)求△F1MF2的面积．
如右图所示，已知圆G：(x－2)2＋y2＝r2是椭圆＋y2＝1的内接△ABC的内切圆，其中A为椭圆的左顶点．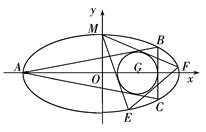
(1)求圆G的半径r；
(2)过点M(0,1)作圆G的两条切线交椭圆于E、F两点，
证明：直线EF与圆G相切．
已知椭圆G的中心在坐标原点，长轴在x轴上，离心率为，两个焦点分别为F1和F2，椭圆G上一点到F1和F2的距离之和为12.圆Ck：x2＋y2＋2kx－4y－21＝0(k∈R)的圆心为点Ak.
(1)求椭圆G的方程；
(2)求△AkF1F2的面积；
(3)问是否存在圆Ck包围椭圆G？请说明理由