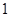(1)几何证明选讲
是
的直径,
为
上一点,过点
作
的切线交
延长线于
,若
,求证
.
(2)矩阵与变换
在平面直角坐标系
中,
,设
,
,点
在矩阵
对应的变换下得到点
的面积是
面积的2倍,求实数
的值
(3)参数方程与极坐标
在极坐标系中,圆
与直线
相切,求实数
的值.
(4)不等式证明选讲
已知实数
,求证:
.
等比数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且a1,a2,a3中的任何两个数不在下表的同一列.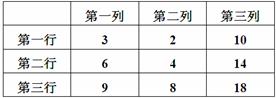
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:bn=an+(-1)nlnan,求数列{bn}的前n项和Sn·
已知数列{an}的前n项和为Sn,且Sn=2an-2(n∈N*),在数列{bn}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上.
(1)求数列{an},{bn}的通项公式;
(2)记Tn=a1b1+a2b2++anbn,求Tn.
在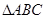 中,角
中,角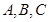 的对边分别为
的对边分别为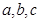 ,
,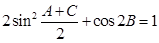
(1)若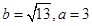 ,求
,求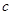 的值;
的值;
(2)设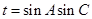 ,当
,当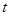 取最大值时求
取最大值时求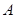 的值。
的值。
在△ABC中,角A,B,C所对的边分别是a,b,c,若sin2B+sin2C=sin2A+sinBsin C,且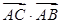 =4,求△ABC的面积S.
=4,求△ABC的面积S.
解关于x的不等式: ≤
≤