在平面直角坐标系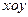 中,如图,已知椭圆
中,如图,已知椭圆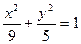 的左右顶点为A,B,右焦点为F,设过点T(
的左右顶点为A,B,右焦点为F,设过点T(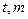 )的直线TA,TB与椭圆分别交于点M
)的直线TA,TB与椭圆分别交于点M ,
, ,其中m>0,
,其中m>0,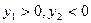
①设动点P满足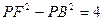 ,求点P的轨迹
,求点P的轨迹
②设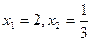 ,求点T的坐标
,求点T的坐标
③设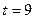 ,求证:直线MN必过x轴上的一定点(其坐标与m无关)
,求证:直线MN必过x轴上的一定点(其坐标与m无关)
 |
选修4—5:不等式选讲
设不等式 的解集为
的解集为 , 且
, 且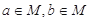 .
.
(Ⅰ) 试比较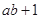 与
与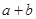 的大小;
的大小;
(Ⅱ) 设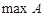 表示数集
表示数集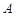 中的最大数, 且
中的最大数, 且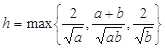 , 求
, 求 的范围.
的范围.
选修4—4:坐标系与参数方程
已知椭圆 C的极坐标方程为
C的极坐标方程为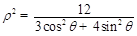 ,点
,点 为其左、右焦点,直线
为其左、右焦点,直线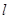 的参数方程为
的参数方程为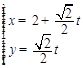 (
( 为参数,
为参数, ).求点
).求点 到直线
到直线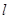 的距离之和.
的距离之和.
选修4—1:几何证明选讲
如图, 内接于⊙
内接于⊙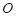 ,
,  是⊙
是⊙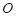 的直径,
的直径,  是过点
是过点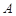 的直线, 且
的直线, 且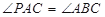 .
.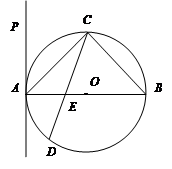
(Ⅰ)求证:  是⊙
是⊙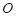 的切线;
的切线;
(Ⅱ)如果弦 交
交 于点
于点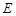 ,
, 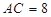 ,
, 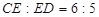 ,
,  , 求
, 求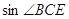 .
.
已知函数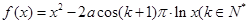 ,
,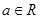 且
且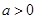 ).
).
(1)讨论函数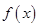 的单调性;
的单调性;
(2)若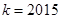 ,方程
,方程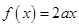 有惟一解时,求
有惟一解时,求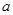 的值。
的值。
已知圆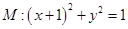 ,圆
,圆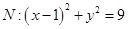 ,动圆
,动圆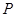 与圆
与圆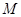 外切并且与圆
外切并且与圆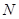 内切,圆心
内切,圆心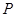 的轨迹为曲线
的轨迹为曲线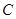 .
.
(1)求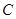 的方程;
的方程;
(2)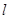 是与圆
是与圆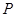 ,圆
,圆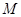 都相切的一条直线,
都相切的一条直线,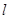 与曲线
与曲线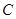 交于
交于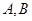 两点,当圆
两点,当圆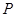 的半径最长时,求
的半径最长时,求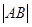 .
.