设数列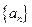 的前
的前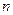 项和为
项和为 。
。
(1)证明: 为等比数列;
为等比数列;
(2)证明:求数列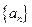 的通项公式;
的通项公式;
(3)确定 与
与 的大小关系,并加以证明。
的大小关系,并加以证明。
已知数列 与
与 ,若
,若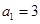 且对任意正整数
且对任意正整数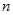 满足
满足 数列
数列 的前n项和
的前n项和 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前n项和
的前n项和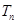 .
.
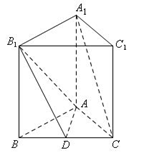
如图,正三棱柱(底面为正三角形,侧棱垂直于底面) 中,D是BC的中点,
中,D是BC的中点, .
.
(Ⅰ)求证: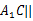 平面
平面 ;
;
(Ⅱ)求点C到平面 的距离.
的距离.
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是: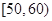 ,
,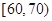 ,
,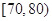 ,
,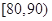 ,
, .
.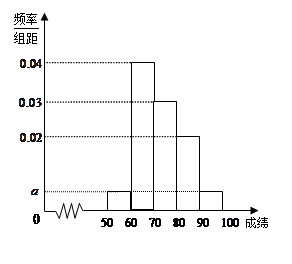
(Ⅰ)求图中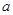 的值;
的值;
(Ⅱ)根据直方图,估计这100名学生语文成绩的平均分;
(Ⅲ)若这100名学生语文成绩某些分数段的人数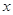 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数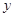 之比如下表所示,求数学成绩在
之比如下表所示,求数学成绩在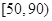 之外的人数.
之外的人数.
| 分数段 |
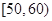 |
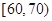 |
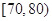 |
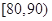 |
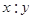 |
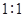 |
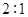 |
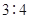 |
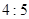 |
已知函数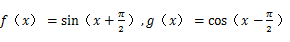 ,则下列结论中正确的是 ()
,则下列结论中正确的是 ()
A.函数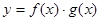 的最小正周期为 的最小正周期为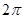 |
B.函数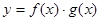 的最大值为1 的最大值为1 |
C.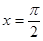 是函数 是函数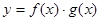 的图象的一条对称轴 的图象的一条对称轴 |
D.函数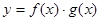 在区间 在区间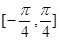 是单调增函数 是单调增函数 |