(本小题13分)已知函数
(1)若实数 求函数
求函数 在
在 上的极值;
上的极值;
(2)记函数 ,设函数
,设函数 的图像
的图像 与
与 轴交于
轴交于 点,曲线
点,曲线 在
在 点处的切线与两坐标轴所围成图形的面积为
点处的切线与两坐标轴所围成图形的面积为 则当
则当 时,求
时,求 的最小值.
的最小值.
(本小题满分14分)已知在平面直角坐标系xoy中的一个椭圆,它的中心在原 。
。
(1)求该椭圆的标准方程;
(2)若P是椭圆上的动点,求线段PA中点M的轨迹方程;
(3)过原点O的直线交椭圆于点B、C,求△ABC面积的最大值。
(本小题满分13分)已知正方体ABCD-A1B1C1D1, O是底ABCD对角线的交点。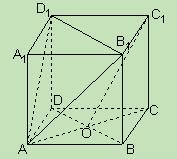
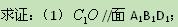
(2)A1C⊥面AB1D1;
(3)求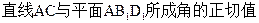
(本小题满分12分)已知:以点 为圆心的圆与x轴交于
为圆心的圆与x轴交于
点O,A,与y轴交于点O,B,其中O为原点。
(Ⅰ) 求证:⊿OAB的面积为定值;
(Ⅱ) 设直线y=-2x+4与圆C交于点M,N,若OM=ON,求圆C的方程。
(本小题满分12分)一个圆锥高h为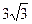 ,侧面展开图是个半圆,求:
,侧面展开图是个半圆,求:
(1)其母线l与底面半径r之比;
(2)锥角 ;
;
(3)圆锥的表面积
已知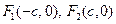 是椭圆
是椭圆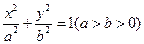 的左、右焦点,过点
的左、右焦点,过点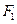 作
作
倾斜角为 的直线
的直线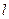 交椭圆于
交椭圆于 两点,
两点, .
.
(1)求椭圆的离心率;
(2)若 ,求椭圆的标准方程.
,求椭圆的标准方程.