(本大题满分14分)
已知数列 和
和 满足:
满足: ,
,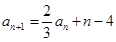 ,
,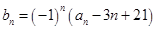 ,其中
,其中 为实数,
为实数, 为正整数.
为正整数.
(Ⅰ)对任意实数 ,证明:数列
,证明:数列 不是等比数列;
不是等比数列;
(Ⅱ)证明:当 时,数列
时,数列 是等比数列;
是等比数列;
(Ⅲ)设 (
( 为实常数),
为实常数), 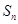 为数列
为数列 的前
的前 项和.是否存在实数
项和.是否存在实数 ,使得对任意正整数
,使得对任意正整数 ,都有
,都有 ?若存在,求
?若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求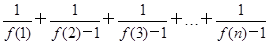 的值.
的值.
设命题p:f(x)=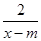 在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若p∧q为真,试求实数m的取值范围.
在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若p∧q为真,试求实数m的取值范围.
已知向量a= ,b=
,b= ,且x∈
,且x∈ .
.
(1)求a·b及|a+b|;
(2)若f(x)=a·b-2λ|a+b|的最小值为- ,求正实数λ的值.
,求正实数λ的值.
若复数z1与z2在复平面上所对应的点关于y轴对称,且z1(3-i)=z2(1+3i),|z1|=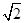 ,求z1.
,求z1.
A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.
(1)求 ·
·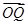 +S的最大值;
+S的最大值;
(2)若CB∥OP,求sin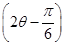 的值.
的值.