已知直线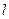 过点P(2,3),并与
过点P(2,3),并与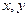 轴正半轴交于A,B二点。
轴正半轴交于A,B二点。
(1)当 AOB面积为
AOB面积为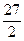 时,求直线
时,求直线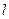 的方程。
的方程。
(2)求 AOB面积的最小值,并写出这时的直线
AOB面积的最小值,并写出这时的直线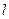 的方程。
的方程。
已知顶点在原点, 焦点在x轴上的抛物线被直线y=2x+1截得的弦长为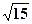 ,求抛物线的方程.
,求抛物线的方程.
.对某电子元件进行寿命追踪调查,情况如下.
| 寿命(h) |
100~200 |
200~300 |
300~400 |
400~500 |
500~600 |
| 个数 |
20 |
30 |
80 |
40 |
30 |
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)估计电子元件寿命在100~400 h以内的在总体中占的比例;
(4)估计电子元件寿命在400 h以上的在总体中占的比例.
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得
他们的最大速度(m/s)的数据如下表.
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |
(1)画出茎叶图
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、标准差,并判断选谁参加比赛更合适.
已知:p:方程x2-mx+1=0有两个不等的正根;q:不等式|x-1|>m的解集为R。若p或q为真命题,p且q为假命题,求实数m的取值范围。
如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,M为线段AB的中点,将△ACD沿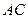 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求二面角A-CD-M的余弦值.