.已知抛物线 的准线为
的准线为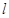 ,焦点为F,
,焦点为F,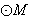 的圆心在
的圆心在 轴的正半轴上,且与
轴的正半轴上,且与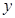 轴相切,过原点O作倾斜角为
轴相切,过原点O作倾斜角为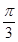 的直线
的直线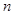 ,交
,交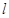 于点A,交
于点A,交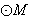 于另一点B,且AO=OB=2.
于另一点B,且AO=OB=2.
(1)求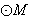 和抛物线C的方程;
和抛物线C的方程;
(2)若P为抛物线C上的动点,求 的最小值;
的最小值;
(3)过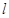 上的动点Q向
上的动点Q向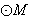 作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
已知|a|<1,|b|<1,|c|<1,求证: abc+2>a+b+c.
某校一年级为配合素质教育,利用一间教室作为学生绘画成果展览室,为节约经费,他们利用课桌作为展台,将装画的镜框放置桌上,斜靠展出,已知镜框对桌面的倾斜角为α(90°≤α<180°)镜框中,画的上、下边缘与镜框下边缘分别相距a m,b m,(a>b). 问学生距离镜框下缘多远看画的效果最佳?
设二次函数f(x)=ax2+bx+c(a>0),方程f(x)-x=0的两个根x1、x2满足0<x1<x2< 。
。
(1)当x∈[0,x1 时,证明x<f(x)<x1;
时,证明x<f(x)<x1;
(2)设函数f(x)的图像关于直线x=x0对称,证明:x0< 。
。
已知a,b,c是实数,函数f(x)=ax2+bx+c,g(x)=ax+b,当-1≤x≤1时|f(x)|≤1。
(1)证明: |c|≤1;
(2)证明:当-1 ≤x≤1时,|g(x)|≤2;
(3)设a>0,有-1≤x≤1时,g(x)的最大值为2,求f(x)。
用一块钢锭烧铸一个厚度均匀,且表面积为2平方米的正四棱锥形有盖容器(如右图)设容器高为h米,盖子边长为a米,
(1)求a关于h的解析式;
(2)设容器的容积为V立方米,则当h为何值时,V最大?求出V的最大值(求解本题时,不计容器厚度)