已知直线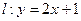 求:
求:
(1)直线关于点M(3,2)的对称的直线方程。
(2)直线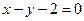 关于
关于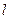 的对称的直线方程。
的对称的直线方程。
如图,在 四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=AD.
四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=AD.
(1)求证:EF∥平面PAD;
(2)求证:直线CD⊥平面PAD
(3)求证:面PAD⊥平面PCD.
为了分析某个高三学生的学习状态,对其下一阶段的学习作出预测和提供指导性建议,现对他前7次考试的数学成绩x、物理成绩y进行分析.下面是该生7次考试的成绩.
| 数学 |
88 |
83 |
117 |
92 |
108 |
100 |
112 |
| 物理 |
94 |
91 |
108 |
96 |
104 |
101 |
106 |
(1)分别求出这个考生的他的数学平均成绩与物理平均成绩,并判断在这个学科中哪科成绩更稳定;
(2)已知该生的物理成绩y与数学成绩x是线性相关的,求出线性回归方程;
(3)若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?
参考公式: ,
,
二次函数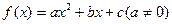 满足
满足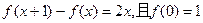 。
。
(1)求函数 的解析式;
的解析式;
(2)在区间 上,
上,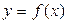
 的图象恒在
的图象恒在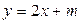 的图象上方,试确定实数
的图象上方,试确定实数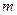 的取值范围。
的取值范围。
每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
按类用分层抽样的方法在这个月生产的 轿车中抽取50辆,其中有A类轿车10辆
轿车中抽取50辆,其中有A类轿车10辆 .
.
(Ⅰ)求z的值.
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将 该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
| 轿车A |
轿车B |
轿 车C 车C |
|
| 舒适型 |
100 |
150 |
z |
| 标准型 |
300 |
450 |
600 |
当实数x为何值时,复数z=x2+x-2+(x2-3x-10)i是
(Ⅰ)虚数;(Ⅱ)纯虚数;(Ⅲ)正实数。