(本小题满分12分)
如图,设 是单位圆和
是单位圆和 轴正半轴的交点,
轴正半轴的交点, 是单位圆上的两点,
是单位圆上的两点, 是坐标原点,
是坐标原点, ,
, .
. 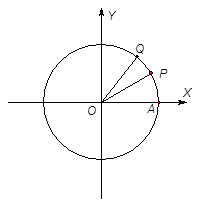
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)设函数 ,求
,求 的值域.
的值域.
在直角坐标系中,射线OA: x-y=0(x≥0),
OB: x+2y=0(x≥0),过点P(1,0)作直线分别交射线OA、OB于A、B两点.
(1)当AB中点为P时,求直线AB的方程;
(2)当AB中点在直线 上时,求直线AB的方程.
上时,求直线AB的方程.
已知四棱锥P-ABCD的直观图(如图(1))及左视图(如图(2)),底面ABCD是边长为2的正方形,平面PAB⊥平面ABCD,PA=PB。
(1)求证:AD⊥PB;
(2)求异面直线PD与AB所成角的余弦值;
(3)求平面PAB与平面PCD所成锐二面角的大小.
已知中心在原点的双曲线C的右焦点为(2,0),右顶点为
(1)求双曲线C的方程;
(2)若直线 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 (其中O为原点). 求k的取值范围.
(其中O为原点). 求k的取值范围.
如图,矩形 中,
中, ,
, ,
, 为
为 上的点,且
上的点,且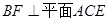 ,AC、BD交于点G.
,AC、BD交于点G.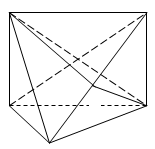
(1)求证: ;
;
(2)求证; ;
;
(3)求三棱锥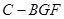 的体积.
的体积.
已知命题p:“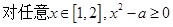 ”,命题q:“
”,命题q:“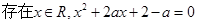 ”若命题“p且q”是真命题,求实数a的取值范围.
”若命题“p且q”是真命题,求实数a的取值范围.