某地区在一年内遭到暴雨袭击的次数用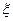 表示,椐统计,随机变量
表示,椐统计,随机变量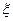 的概率分布如下:
的概率分布如下:
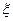 |
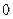 |
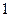 |
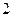 |
 |
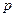 |
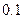 |
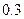 |
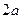 |
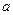 |
(1)求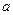 的值和
的值和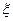 的数学期望;
的数学期望;
(2)假设第一年和第二年该地区遭到暴雨的次数互不影响,求这两年内该地区共遭到暴雨袭击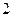 次的概率。
次的概率。
如图:已知长方体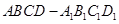 的底面
的底面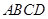 是边长为
是边长为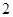 的正方形,高
的正方形,高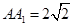 ,
,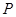 为
为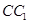 的中点,
的中点,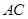 与
与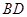 交于
交于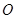 点.
点.
(1)求证: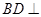 平面
平面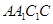 ;
;
(2)求证: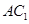 ∥平面
∥平面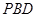 ;
;
(3)求三棱锥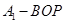 的体积.
的体积.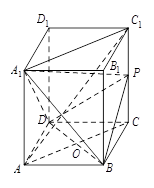
甲、乙两名运动员参加“选拔测试赛”,在相同条件下,两人5次测试的成绩(单位:分)记录如下:
甲 86 77 92 72 78
乙 78 82 88 82 95
(1)用茎叶图表示这两组数据;.
(2)现要从中选派一名运动员参加比赛,你认为选派谁参赛更好?说明理由(不用计算);
(3)若从甲、乙两人的5次成绩中各随机抽取一个,求甲的成绩比乙高的概率.
已知函数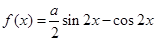 的图象过点
的图象过点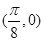 .
.
(1)求实数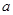 的值;
的值;
(2)求函数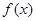 的最小正周期及最大值.
的最小正周期及最大值.
已知集合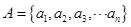 ,
,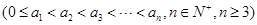
具有性质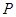 :对任意的
:对任意的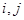
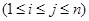 ,
,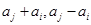 至少有一个属于
至少有一个属于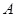 .
.
(1)分别判断集合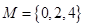 与
与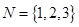 是否具有性质
是否具有性质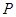 ;
;
(2)求证:①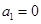 ;
;
②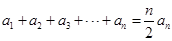 ;
;
(3)当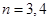 或
或 时集合
时集合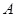 中的数列
中的数列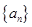 是否一定成等差数列?说明理由.
是否一定成等差数列?说明理由.
已知椭圆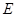 的两个焦点分别为
的两个焦点分别为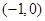 和
和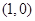 ,离心率
,离心率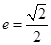 .
.
(1)求椭圆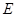 的方程;
的方程;
(2)设直线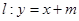 (
(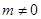 )与椭圆
)与椭圆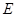 交于
交于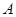 、
、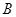 两点,线段
两点,线段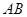 的垂直平分线交
的垂直平分线交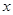 轴于点
轴于点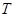 ,当
,当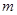 变化时,求
变化时,求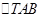 面积的最大值.
面积的最大值.