已知函数
。
(I)当
时,求曲线
在点
处的切线方程。
(II)设
是
的两个极值点,
是
的一个零点,且
,证明:存在实数
,使得
按某种顺序排列后的等差数列,并求
.
已知函数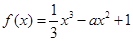
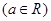 .
.
(Ⅰ)若曲线y=f(x)在(1,f(1))处的切线与直线x+y+1=0平行,求a的值;
(Ⅱ)若a>0,函数y=f(x)在区间(a,a 2-3)上存在极值,求a的取值范围;
(Ⅲ)若a>2,求证:函数y=f(x)在(0,2)上恰有一个零点.
某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量。若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”。若小区内有至少75%的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”。已知备选的5个居民小区中有三个非低碳小区,两个低碳小区。
(I)求所选的两个小区恰有一个为“非低碳小区”的概率;
(Ⅱ)假定选择的“非低碳小区”为小区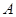 ,调查显示其“低碳族”的比例为
,调查显示其“低碳族”的比例为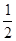 ,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区
,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区 是否达到“低碳小区”的标准?
是否达到“低碳小区”的标准?
边长为2的正方形ABCD所在平面外有一点P,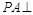 平面ABCD,
平面ABCD,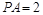 ,E是PC上的一点.
,E是PC上的一点.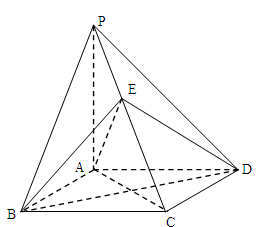
(Ⅰ)求证:AB//平面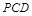 ;
;
(Ⅱ)求证:平面 平面
平面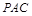 ;
;
(Ⅲ)线段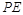 为多长时,
为多长时,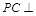 平面
平面 ?
?
已知向量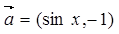 ,
,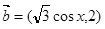 ,函数
,函数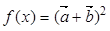 .
.
(Ⅰ)求函数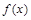 的最小正周期;(Ⅱ)若
的最小正周期;(Ⅱ)若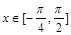 ,求函数
,求函数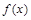 的值域。
的值域。
已知等差数列 中,
中, ,
, ,数列
,数列 中,
中, ,
, .
.
(Ⅰ)求数列 的通项公式,写出它的前
的通项公式,写出它的前 项和
项和 ;
;
(Ⅱ)求数列 的通项公式。
的通项公式。