(本小题满分12分)
设椭圆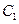 :
: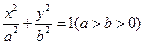 ,抛物线
,抛物线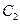 :
: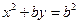 .
.
(1) 若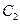 经过
经过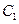 的两个焦点,求
的两个焦点,求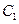 的离心率;
的离心率;
(2) 设 ,又
,又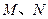 为
为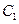 与
与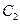 不在
不在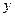 轴上的两个交点,若
轴上的两个交点,若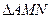 的垂心为
的垂心为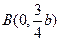 ,且
,且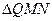 的重心在
的重心在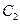 上,求椭圆
上,求椭圆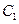 和抛物线
和抛物线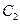
 的方程.
的方程.
在对人们休闲的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)画出三维柱形图和二维条形图;
(3)检验性别是否与休闲方式有关,可靠性有多大.
把4个球随机地投入4个盒子中去,设ξ表示空盒子的个数,求ξ的分布列.
已知男人中有5%患色盲,女人中有0.25%患色盲,从100个男人和100个女人中任选一人.
(1)求此人患色盲的概率;
(2)如果此人是色盲,求此人是男人的概率.
袋中装有一些大小相同的球,其中有号数为1的球1个,号数为2的球2个,号数为3的球3个,…,号数为n的球n个.从袋中任取一球,其号数作为随机变量ξ,求ξ的概率分布和期望.
人寿保险中(某一年龄段),在一年的保险期内,每个被保险人需交纳保费a元,被保险人意外死亡则保险公司赔付3万元,出现非意外死亡则赔付1万元。经统计此年龄段一年内意外死亡的概率是p1,非意外死亡的概率为p2,则a需满足什么条件,保险公司才可能盈利.