已知函数
的图像在点
处的切线方程为
.
(Ⅰ)求实数
的值;
(Ⅱ)设
是
上的增函数.
(ⅰ)求实数
的最大值;
(ⅱ)当
取最大值时,是否存在点Q,使得过点Q的直线能与曲线
围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由.
已知函数
.
(Ⅰ)当
时,求不等式
的解集;
(Ⅱ)设
,且当
时,
,求
的取值范围.
已知曲线
的参数方程为
(
为参数),以坐标原点为极点,
轴的正半轴为极轴建立极坐标系,曲线
的极坐标方程为
。
(Ⅰ)把
的参数方程化为极坐标方程;
(Ⅱ)求
与
交点的极坐标
【选修4-1:几何证明选讲】
如图,直线
为圆的切线,切点为
,点
在圆上,
的角平分线BE交圆于点
,
垂直
交圆于
.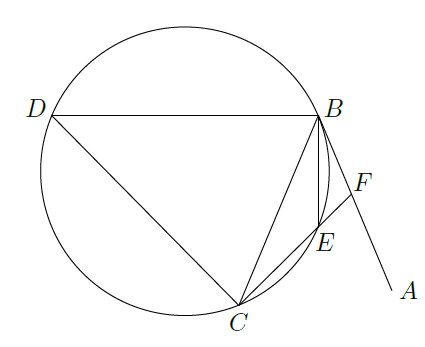
(Ⅰ)证明:
;
(Ⅱ)设圆的半径为1,
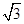 ,延长
交
于点
,求
外接圆的半径.
,延长
交
于点
,求
外接圆的半径.
已知函数 ,若曲线 和曲线 都过点 ,且在点 处有相同的切线 .
(Ⅰ)求
的值
(Ⅱ)若
时,
,求
的取值范围。
已知圆
,圆
,动圆
与圆
外切并与圆
内切,圆心
的轨迹为曲线
.
(Ⅰ)求
的方程;
(Ⅱ)l是与圆
,圆
都相切的一条直线,l与曲线
交于
两点,当圆
的半径最长时,求
.