已知是给定的实常数,设函数,,是的一个极大值点.
(Ⅰ)求的取值范围;
(Ⅱ)设是的3个极值点,问是否存在实数,可找到,使得的某种排列(其中)依次成等差数列?若存在,求所有的及相应的;若不存在,说明理由.
某重点高校数学教育专业的三位毕业生甲、乙、丙参加了一所中学的招聘面试,
面试合格者可以正式签约,毕业生甲表示只要面试合格就签约,毕业生乙和丙则约定:两人
面试都合格就一同签约,否则两人都不签约,设每人面试合格的概率都是 ,且面试是否合
,且面试是否合
格互不影响,求:(I)至少有1人面试合格的概率;(II)签约人数 的分布列和数学期望。
的分布列和数学期望。
设函数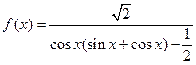 (I)求函数
(I)求函数 的周期;(II)设函数
的周期;(II)设函数 的定义域为
的定义域为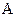 ,若
,若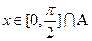 ,求函数
,求函数 的值域。
的值域。
如图所示,四棱锥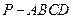 中,
中,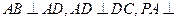 底面
底面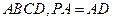
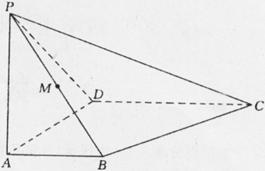
 为
为 的中点。
的中点。
(I)试在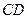 上确定一点
上确定一点 ,使得
,使得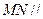 平面
平面 (II)点
(II)点 在满足(I)的条件下,求直线
在满足(I)的条件下,求直线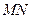 与平面
与平面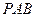 所成角的正弦值。
所成角的正弦值。
甲乙两人进行一种游戏,两人同时随机地喊出杠、虎、鸡、虫,按照杠打虎、虎吃鸡、鸡捉虫、虫啃杠的原则决定胜负,(比如甲喊杠的同时,乙若喊虎则乙输,乙若喊虫则乙嬴,乙若喊杠或鸡则不分胜负。)若两人同时喊出一次后不分胜负则继续喊下去,直到分出胜负
(I)喊一次甲就获胜的概率是多少?(II)甲在喊不超过三次的情况下就获胜的概率是多少?
(13)已知函数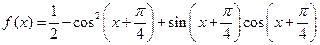
(I)求函数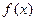 的最大值和周期;(II)设角
的最大值和周期;(II)设角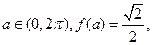 求
求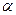 。
。