某重点高校数学教育专业的三位毕业生甲、乙、丙参加了一所中学的招聘面试,
面试合格者可以正式签约,毕业生甲表示只要面试合格就签约,毕业生乙和丙则约定:两人
面试都合格就一同签约,否则两人都不签约,设每人面试合格的概率都是 ,且面试是否合
,且面试是否合
格互不影响,求:(I)至少有1人面试合格的概率;(II)签约人数 的分布列和数学期望。
的分布列和数学期望。
(1)已知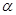 是第二象限角,且
是第二象限角,且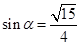 ,求
,求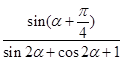 的值.
的值.
(2)已知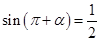 ,求
,求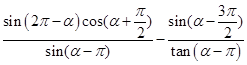 的值。
的值。
函数 ,数列
,数列 的前n项和
的前n项和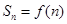 ,且
,且 同时满足:
同时满足:
① 不等式 ≤ 0的解集有且只有一个元素;
≤ 0的解集有且只有一个元素;
② 在定义域内存在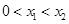 ,使得不等式
,使得不等式 成立.
成立.
(1) 求函数 的表达式;
的表达式;
(2) 求数列 的通项公式.
的通项公式.
已知函数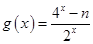 是奇函数,
是奇函数, 是偶函数。
是偶函数。
(1)求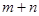 的值;
的值;
(2)设 若
若 对任意
对任意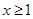 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
已知二次函数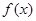 的二次项系数为
的二次项系数为 ,满足不等式
,满足不等式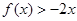 的解集为(1,3),且方程
的解集为(1,3),且方程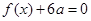 有两个相等的实根,求
有两个相等的实根,求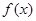 的解析式.
的解析式.
某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?