（本小题满分12分）下图是某市今年1月份前30天空气质量指数（AQI）的趋势图.
（1）根据该图数据在答题卷中完成频率分布表，并在图中补全这些数据的频率分布直方图；
（2）当空气质量指数（AQI）小于100时，表示空气质量优良．某人随机选择当月（按30天计）某一天
到达该市，根据以上信息，能否认为此人到达当天空气质量优良的可能性超过60%？
（本小题满分13分）
已知数列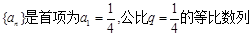
，设 
，数列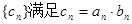
．
（I）求证：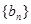
是等差数列；
（II）求数列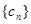
的前n项和Sn；
（Ⅲ）若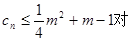
一切正整数n恒成立，求实数m的取值范围．
（本小题满分13分）
抛物线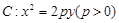
上一点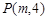
到其焦点的距离为5．
（I）求
与
的值；
（II）若直线
与抛物线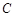
相交于
、
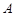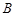两点，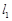
、
分别是该抛物线在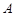、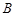两点处的切线，
、
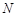分别是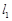、与该抛物线的准线交点，求证：
．
（本小题满分13分）已知函数
，其中
为自然对数的底数.
（Ⅰ）当
时，求曲线
在
处的切线与坐标轴围成的面积；
（Ⅱ）若函数
存在一个极大值点和一个极小值点，且极大值与极小值的积为
，求
的值.
（本小题满分12分）科研所研究人员都具有本科和研究生两类学历,年龄段和学历如下表,从该科研所任选一名研究人员,是本科生概率是
,是35岁以下的研究生概率是
.
（Ⅰ）求出表格中的
和
的值;
（Ⅱ）设“从数学教研组任选两名教师,本科一名,研究生一名,50岁以上本科生和35岁以下的研究生不全选中” 的事件为A,求事件A概率P(A).
（本小题满分12分）
如图，已知棱柱
的底面是菱形，且
面
，
，
=１，
为棱
的中点，
为线段
的中点．
（Ⅰ）求证：
面；
（Ⅱ）试判断直线ＭＦ与平面
的位置关系，并证明你的结论；
（Ⅲ）求三棱锥
的体积．