为了对某课题进行研究,用分层抽样方法从三所高校
的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)
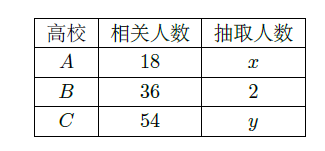
(I)求
;
(II)若从高校
抽取的人中选2人作专题发言,求这二人都来自高校
的概率。
已知定义域为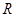 的奇函数
的奇函数 ,当
,当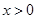 时,
时,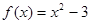 .
.
(1)当 时,求函数
时,求函数 的解析式;
的解析式;
(2)求函数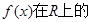 解析式;
解析式;
(3)解方程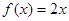 .
.
已知函数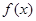 是
是 上的奇函数,当
上的奇函数,当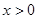 时,
时,
(1)当 时,求函数
时,求函数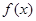 的解析式;
的解析式;
(2)证明函数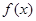 在区间
在区间 上是单调增函数.
上是单调增函数.
已知全集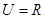 ,集合
,集合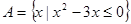 ,
,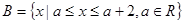
(1)当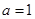 时,求
时,求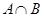 ;
;
(2)当集合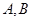 满足
满足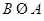 时,求实数
时,求实数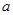 的取值范围.
的取值范围.
(本小题满分16分)已知数列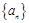 的前
的前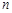 项和
项和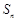 满足:
满足: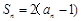 ,数列
,数列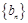 满足:对任意
满足:对任意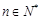 有
有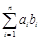
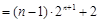 .
.
(1)求数列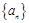 与数列
与数列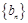 的通项公式;
的通项公式;
(2)记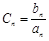 ,数列
,数列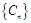 的前
的前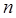 项和为
项和为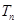 ,证明:当
,证明:当 时,
时,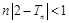 .
.
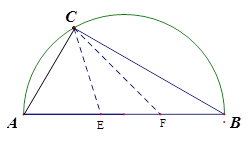
(本小题满分16分)如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植甲水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的 处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是
处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是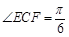 ,点
,点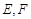 在直径
在直径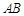 上,且
上,且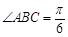 .
.
(1)若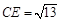 ,求
,求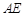 的长;
的长;
(2)设 , 求该空地产生最大经济价值时种植甲种水果的面积.
, 求该空地产生最大经济价值时种植甲种水果的面积.