在△ABC中,角A、B、C的对边分别为a、b、c,且满足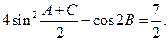
(Ⅰ)求角B的度数;
(Ⅱ)如果b = ,a + c = 3且a>c,求a、c的值.
,a + c = 3且a>c,求a、c的值.
已知函数 .
.
(1)当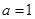 时,求函数
时,求函数 的图像在
的图像在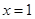 处的切线方程;
处的切线方程;
(2)若在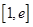 (
( 为自然对数的底数)上存在一点
为自然对数的底数)上存在一点 ,使得
,使得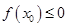 成立,求实数
成立,求实数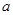 的取值范围.
的取值范围.
已知椭圆 的中心在坐标原点,短轴长为4,且有一个焦点与抛物线
的中心在坐标原点,短轴长为4,且有一个焦点与抛物线 的焦点重合.
的焦点重合.
(1)求椭圆 的方程;
的方程;
(2)已知过定点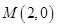 且斜率不为0的直线
且斜率不为0的直线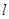 交椭圆
交椭圆 于
于 两点,试问在
两点,试问在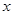 轴上是否存在一个定点
轴上是否存在一个定点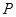 使得
使得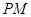 始终平分
始终平分 ?若存在,求出点
?若存在,求出点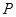 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
如图,正三棱锥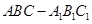 的所有棱长都为2,
的所有棱长都为2,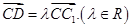 .
.
(1)当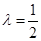 时,求证:
时,求证: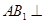 平面
平面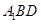 ;
;
(2)当二面角 的大小为
的大小为 时,求实数
时,求实数 的值.
的值.
威力实施“爱的教育”实践活动,宇华教育集团决定举行“爱在宇华”教师演讲比赛.焦作校区决定从高中部、初中部、小学部和幼教部这四个部门选出12人组成代表队代表焦作校区参赛,选手来源如下表:
| 部门 |
高中部 |
初中部 |
小学部 |
幼教部 |
| 人数 |
4 |
4 |
2 |
2 |
焦作校区选手经过出色表现获得冠军,现要从中选出两名选手代表冠军队发言.
(1)求这两名队员来自同一部门的概率;
(2)设选出的两名选手中来自高中部的人数为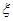 ,求随机变量
,求随机变量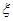 的分布列及数学期望
的分布列及数学期望 .
.
已知等差数列 的各项互不相等,前两项的和为10,设向量
的各项互不相等,前两项的和为10,设向量 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 的前
的前 项和为
项和为 ,求证:
,求证: