(本小题满分15分)已知
(Ⅰ)求 的表达式;
的表达式;
(Ⅱ)定义正数数列 ,证明:数列
,证明:数列 是等比数列;
是等比数列;
|
(Ⅲ)令 成立的最小n值.
成立的最小n值.
已知命题 若
若 是
是 的充分不必要条件,求
的充分不必要条件,求 的取值范围
的取值范围
(本小题 分)
分)
设 是数列
是数列 的前
的前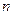 项和,点
项和,点
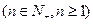 在直线
在直线 上.
上.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)记 ,数列
,数列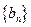 的前
的前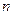 项和为
项和为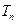 ,求使
,求使 的
的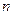 的最小值;
的最小值;
(Ⅲ)设正数数列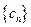 满足
满足 ,求数列
,求数列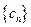 中的最大项.
中的最大项.
(本小题满分  分)
分)
已知直线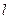 与抛物线
与抛物线 相切于点
相切于点 ,且与
,且与 轴交于点
轴交于点 ,定点
,定点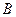 的坐标为
的坐标为 .
.
(Ⅰ)若动点 满足
满足 ,求点
,求点 的轨迹
的轨迹 ;
;
(Ⅱ)若过点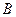 的直线
的直线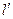 (斜率不等于零)与(I)中的轨迹
(斜率不等于零)与(I)中的轨迹 交于不同的两点
交于不同的两点 、
、 (
( 在
在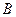 、
、 之间),试求
之间),试求 与
与 面积之比的取值范围.
面积之比的取值范围.
(本小题满分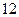 分)
分)
设函数 .
.
(Ⅰ)求函数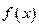 单调区间;
单调区间;
(Ⅱ)若 恒成立,求
恒成立,求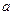 的取值范围;
的取值范围;
(本小题满分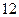 分)
分)
如图,在四棱柱ABCD—A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D= ,底面ABCD为直角梯形,其中BC//AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC//AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:A1O//平面AB1C;
(Ⅱ)求锐二面角A—C1D1—C的余弦值.