已知数列 满足: , , ;数列 满足: .
(1)求数列 , 的通项公式;
(2)证明:数列 中的任意三项不可能成等差数列。
已知数列 满足,
满足,
证明: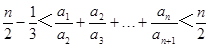 ,(
,(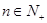 )
)
在一个特定时段内,以点E为中心的7n mile以内海域被设为警戒水域.点E正北55n mile处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40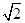 n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东
n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东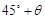 (其中
(其中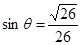 ,
, )且与点A相距10
)且与点A相距10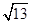 n mile的位置C.
n mile的位置C.
(I)求该船的行驶速度(单位:n mile /h);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
已知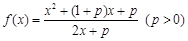
(1)若p >1时,解关于x的不等式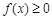 ;
;
(2)若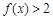 对
对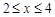 时恒成立,求p的范围.
时恒成立,求p的范围.
如图,在四棱锥 中,
中,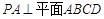 ,
, ,且
,且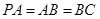 ,E是PC的中点.
,E是PC的中点.
(1)证明: ;
;
(2)证明: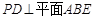 ;
;
已知: 是
是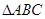 的内角,
的内角, 分别是其对边长,向量
分别是其对边长,向量 ,
, ,
, .
.
(Ⅰ)求角A的大小;
(Ⅱ)若 求
求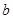 的长.
的长.