已知数列满足a1=0,a2=2,且对任意都有
(Ⅰ)求;
(Ⅱ)设,证明:是等差数列;
(Ⅲ)设,求数列的前n项和.
已知各项均不相等的等差数列{an}的前5项和为S5=35,且a1+1,a3+1,a7+1成等比数列.
(1)求数列{an}的通项公式;
(2)设Tn为数列 的前n项和,问是否存在常数m,使Tn=m
的前n项和,问是否存在常数m,使Tn=m ,若存在,求m的值;若不存在,说明理由.
,若存在,求m的值;若不存在,说明理由.
设等比数列{an}的前n项和为Sn,a4=a1-9,a5,a3,a4成等差数列.
(1)求数列{an} 的通项公式;
(2)证明:对任意k∈N*,Sk+2,Sk,Sk+1成等差数列.
在等腰梯形ABCD中,AD∥BC,AD=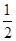 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).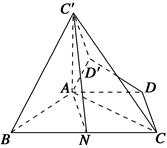
(1)求证:AC⊥平面ABC′;
(2)求证:C′N∥平面ADD′;
(3)求二面角A-C′N-C的余弦值.
如图,在四棱锥P-ABCD中,平面PAC⊥平面ABCD,且PA⊥AC,PA=AD=2.四边形ABCD满足BC∥AD,AB⊥AD,AB=BC=1.点E,F分别为侧棱PB,PC上的点,且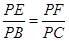 =λ.
=λ.
(1)求证:EF∥平面PAD.
(2)当λ= 时,求异面直线BF与CD所成角的余弦值;
时,求异面直线BF与CD所成角的余弦值;
(3)是否存在实数λ,使得平面AFD⊥平面PCD?若存在,试求出λ的值;若不存在,请说明理由.
在正三棱柱ABC-A1B1C1中,AB=2,AA1=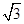 ,点D为AC的中点,点E在线段AA1上.
,点D为AC的中点,点E在线段AA1上.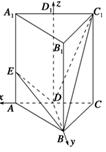
(1)当AE∶EA1=1∶2时,求证DE⊥BC1;
(2)是否存在点E,使二面角D-BE-A等于60°,若存在求AE的长;若不存在,请说明理由.