设计一幅宣传画,要求画面面积为 ,画面的宽与高的比为
,画面的宽与高的比为 ,画面的上
,画面的上
各留 的空白,左右各留
的空白,左右各留 的空白,问怎样确定画面的高与宽的尺寸,能使宣传画
的空白,问怎样确定画面的高与宽的尺寸,能使宣传画
所用纸张面积最小?如果 ,那么
,那么 为何值时,能使宣传画所用纸张面积最小?
为何值时,能使宣传画所用纸张面积最小?
(本小题满分12分)
口袋中有6个大小相同的小球,其中1个小球标有数字“3”,2个小球标有数字“2”,3个小球标有数字“1”,每次从中任取一个小球,取后放回,连续抽取两次。
(I)求两次取出的小球所标数字不同的概率;
(II)记两次取出的小球所标数字之和为 ,求
,求 的分布列和期望。
的分布列和期望。
(本小题满分10分)7.
在 中,角A、B、C的对边分别为a、b、c,已知
中,角A、B、C的对边分别为a、b、c,已知 ,
, ,求b边的长。
,求b边的长。
已知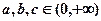 ,且
,且 ,求
,求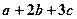 的最小值及取得最小值时
的最小值及取得最小值时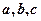 的值
的值
在直角坐标系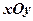 中,以
中,以 为极点,
为极点,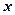 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线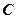 的极坐标方程为
的极坐标方程为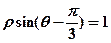 ,
,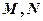 分别为曲线
分别为曲线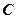 与
与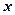 轴,
轴,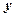 轴的交点.
轴的交点.
(1)写出曲线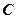 的直角坐标方程,并求出
的直角坐标方程,并求出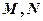 的极坐标;
的极坐标;
(2)设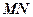 的中点为
的中点为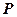 ,求直线
,求直线 的极坐标方程.
的极坐标方程.
在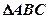 中,已知
中,已知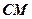 是
是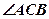 的角平分线,
的角平分线, 的外接圆交
的外接圆交 于点
于点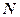 ,
, .求证:
.求证: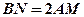 .
.