(本小题满分6分)已知函数
(1)写出函数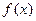 的周期;
的周期;
(2)将函数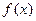 图像上所有的点向右平移
图像上所有的点向右平移 个单位,得到函数
个单位,得到函数 的图像,写出函数
的图像,写出函数 的表达式,并判断函数
的表达式,并判断函数 的奇偶性.
的奇偶性.
(本小题满分12分)设椭圆 的左右焦点分别为
的左右焦点分别为 、
、 ,
, 是椭圆
是椭圆 上的一点,
上的一点, ,坐标原点
,坐标原点 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆 的方程;
的方程;
(2)设 是椭圆
是椭圆 上的一点,
上的一点, ,连接QN的直线交
,连接QN的直线交 轴于点
轴于点 ,若
,若 ,求直线
,求直线 的斜率.
的斜率.
(本小题满分12分)(理科做)在四棱锥P-ABCD中,侧面PCD 底面ABCD,PD
底面ABCD,PD CD,底面ABCD是直角梯形,AB∥DC,
CD,底面ABCD是直角梯形,AB∥DC, ,
, ,
, .
.
(1)求证:BC 平面PBD:
平面PBD:
(2)求直线AP与平面PDB所成角的正弦值;
(3)设E为侧棱PC上异于端点的一点, ,试确定
,试确定 的值,使得二面角E-BD-P的余弦值为
的值,使得二面角E-BD-P的余弦值为 .
.
(文科做)已知函数 在点
在点 的切线方程为
的切线方程为 .
.
(1)求函数 的解析式;
的解析式;
(2)设 ,求证:
,求证: 在
在 上恒成立.
上恒成立.
(本小题满分12分)各项均不相等的等差数列 的前四项的和为
的前四项的和为 ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式
的通项公式 与前n项和
与前n项和 ;
;
(2)记 为数列
为数列 的前n项和,求
的前n项和,求
(本小题满分12分)已知双曲线 的离心率为
的离心率为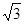 ,点
,点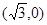 是双曲线的一个顶点.
是双曲线的一个顶点.
(1)求双曲线的方程;
(2)经过的双曲线右焦点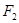 作倾斜角为30°直线
作倾斜角为30°直线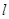 ,直线
,直线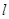 与双曲线交于不同的
与双曲线交于不同的 两点,求
两点,求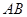 的长.
的长.
(本小题共12分)△ABC的三个内角A,B,C的对边分别为a,b,c,且△ABC的面积为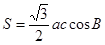 .
.
(1)若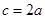 ,求角A,B,C的大小;
,求角A,B,C的大小;
(2 )若a=2,且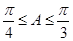 ,求边c的取值范围.
,求边c的取值范围.