【物理-物理3-5】
（1）大量氢原子处于不同能量激发态，发生跃迁时放出三种不同能量的光子，其能量值分别是：
。跃迁发生前这些原子分布在个激发态能级上，其中最高能级的能量值是（基态能量为）。
（2）如图所示，滑块质量均为，滑块质量为。开始时分别以的速度沿光滑水平轨道向固定在右侧的挡板运动，现将无初速地放在上，并与粘合不再分开，此时与相距较近，与挡板碰撞将以原速率反弹，与碰撞将粘合在一起。为使能与挡板碰撞两次，应满足什么关系？
如右图a所示,间距为d的平行金属板MN与一对光滑的平行导轨相连,平行导轨间距L=d/2，一根导体棒ab以一定的初速度向右匀速运动，棒的右端存在一个垂直纸面向里，大小为B的匀强磁场。棒进入磁场的同时，粒子源P释放一个初速度为0的带电粒子，已知带电粒子质量为m,电量为q.粒子能从N板加速到M板，并从M板上的一个小孔穿出。在板的上方，有一个环形区域内存在大小也为B，垂直纸面向外的匀强磁场。已知外圆半径为2d， 里圆半径为d. 两圆的圆心与小孔重合（粒子重力不计）
（1）判断带电粒子的正负，并求当ab棒的速度为vo时，粒子到达M板的速度v；
（2）若要求粒子不能从外圆边界飞出，则v0的取值范围是多少？
(3) 若棒ab的速度v0只能是
，则为使粒子不从外圆飞出，则可以控制导轨区域磁场的宽度S（如图b所示），那该磁场宽度S应控制在多少范围内
工厂里有一种运货的过程可以简化为如图所示,货物m=20kg，以初速度V0=10m/s滑上静止的小车M，M=30kg，货车高h=0.8m。在光滑的轨道OB上设置一固定的障碍物，当货车撞到障碍物时会被粘住不动，而货物就被抛出，恰好会沿BC方向落在B点，已知货车上表面的动摩擦因数
，斜面的倾角为53°（
，g=10m/s2）
(1)求货物从A到B点的时间
（2）求AB之间的水平距离
（3）若已知OA段距离足够长，导致货车在碰到A之前已经与货物达到共同速度，则货车的长度是多少
如图，两光滑导体框ABCD与EFGH固定在水平面内，在D点平滑接触，A、C分别处于FE、HG的沿长线上，ABCD是边长为a的正方形；磁感强度为B的匀强磁场竖直向上；导体棒MN置于导体框上与导体框良好接触，以速度v沿BD方向从B点开始匀速运动，已知线框ABCD及棒MN单位长度的电阻为r，线框EFGH电阻不计。求：
⑴导体棒MN在线框ABCD上运动时，通过MN电流的最大值与最小值；
⑵为维持MN在线框ABCD上的匀速运动，必须给MN施加一水平外力，用F（t）函数表示该力；
⑶导体棒达D点时立即撤去外力，则它还能前进多远（设EF、GH足够长）？
如图所示，真空室内存在宽度为d=8cm的匀强磁场区域，磁感应强度B=0.332T，磁场方向垂直于纸面向里；ab、cd足够长，cd为厚度不计的金箔，金箔右侧有一匀强电场区域，电场强度E=3.32×105N/C；方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S，可沿纸面向各个方向均匀放射初速率相同的α粒子，已知：α粒子的质量m=6.64×10－27kg，电荷量q =＋3.2×10－19C，初速度v = 3.2×106m/s。不计粒子重力（sin37°= 0.6，cos37°= 0.8）求：
（1）α粒子在磁场中作圆周运动的轨道半径R；
（2）金箔cd被α粒子射中区域的长度L；
（3）设打在金箔上d端离cd中心最远的α粒子，速度方向不变穿出金箔进入电场。在电场中运动通过N点，SN⊥ab且SN = 40cm，则此α粒子从金箔上穿出时的速度大小为多少？
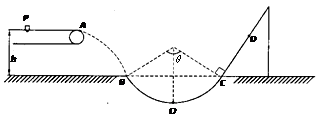
质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点，随传送带运动到A点后水平抛出，小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆孤轨道下滑。B、C为圆弧的两端点，其连线水平，斜面与圆弧轨道在C点相切连接（小物块经过C点时机械能损失不计）。已知圆弧半径R="1.0" m，圆弧对应圆心角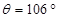
，轨道最低点为O，A点距水平面的高度h=0.8m。设小物块首次经过C点时为零时刻，在t=0.8s时刻小物块经过D点，小物块与斜面间的滑动摩擦因数为
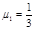。（g=10m/s2，sin37°=0.6，cos37°=0.8）试求：
⑴小物块离开A点的水平初速度vA大小；
⑵小物块经过O点时对轨道的压力；
⑶斜面上CD间的距离。