(本题满分14分袋中有大小相同的红、黄两种颜色的球各 个,从中任取
个,从中任取 只,有放回地抽取
只,有放回地抽取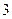 次
次 求: ①
求: ①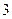 只全是红球的概率; ②
只全是红球的概率; ②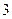 只颜色全相同的概率;③
只颜色全相同的概率;③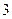 只颜色不全相同的概率
只颜色不全相同的概率
(本小题满分12分)
已知数列 满足
满足 ,数列
,数列 满足
满足 ,
,
数列 满足
满足 .
.
(1)若 ,证明数列
,证明数列 为等比数列;
为等比数列;
(2)在(1)的条件下,求数列 的通项公式;
的通项公式;
(3)若 ,证明数列
,证明数列 的前
的前 项和
项和 满足
满足 。
。
(本小题满分12分)
已知椭圆C中心在原点,焦点在 轴上,一条经过点
轴上,一条经过点 且倾斜角余弦值为
且倾斜角余弦值为 的直线
的直线 交椭圆于A,B两点,交
交椭圆于A,B两点,交 轴于M点,又
轴于M点,又 .
.
(1)求直线 的方程;
的方程;
(2)求椭圆C长轴的取值范围。
(本小题满分12分)
正项单调数列 的首项为
的首项为 ,
, 时,
时, ,数列
,数列 对任意
对任意 均有
均有
(1)求证:数列 是等差数列;
是等差数列;
(2)已知 ,数列
,数列 满足
满足 ,记数列
,记数列 的前
的前 项和为
项和为 ,求证
,求证 .
.
(本小题满分12分)
双曲线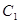 与双曲线
与双曲线 有共同的渐近线,且经过点
有共同的渐近线,且经过点 ,椭圆
,椭圆 以双曲线
以双曲线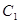 的焦点为焦点且椭圆上的点与焦点的最短距离为
的焦点为焦点且椭圆上的点与焦点的最短距离为 ,求双曲线
,求双曲线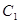 和椭圆
和椭圆 的方程。
的方程。
(本小题满分12分)
某投资人打算投资甲、乙两个项目.根据预测,甲、乙两个项目最大盈利率分为 100%和50%,可能的最大亏损率分别为30%和10%.投资人计划投入的资金额不超过10万元.如果要求确保可能的投入资金的亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能产生的盈利最大?