(本小题满分14分)
已知函数
(1)求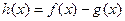 的单调区间;
的单调区间;
(2)求证:当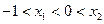 时,
时,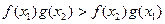 ;
;
(3)求证:
(本小题满分12分)
已知函数
(1)若 求
求 的单调区间及
的单调区间及 的最小值;
的最小值;
(2)求 的单调区间;
的单调区间;
(3)试比较 的大小,
的大小, ,并证明你的结论。
,并证明你的结论。
(本小题满分12)
设二次函数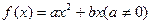 满足条件:
满足条件:
①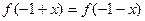 ;②函数
;②函数 的图象与直线
的图象与直线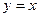 只有一个公共点。
只有一个公共点。
(1)求 的解析式;
的解析式;
(2)若不等式 时恒成立,求实数
时恒成立,求实数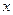 的取值范围。
的取值范围。
(本小题满分12分)
为保增长、促发展,某地计划投资甲、乙两项目,市场调研得知,甲项目每投资百万元需要配套电能2万千瓦,可提供就业岗位24个,增加GDP260万元;乙项目每项投资百万元需要配套电能4万千瓦,可提供就业岗位32个,增加GDP200万元,已知该地为甲、乙两项目最多可投资3000万元,配套电能100万千瓦,并要求它们提供的就业岗位不少于800个,如何安排甲、乙两项目的投资额,增加的GDP最大?
(本小题满分12分)
设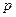 :函数
:函数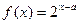 在区间(4,+∞)上单调递增;
在区间(4,+∞)上单调递增;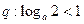 ,如果“
,如果“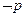 ”是真命题,“
”是真命题,“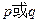 ”也是真命题,求实数
”也是真命题,求实数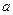 的取值范围。
的取值范围。