如图,椭圆
的顶点为
,焦点为
,
.

(Ⅰ)求椭圆
的方程;
(Ⅱ)设
为过原点的直线,
是与
垂直相交于
点,与椭圆相交于
两点的直线,
.是否存在上述直线
使
成立?若存在,求出直线
的方程;并说出;若不存在,请说明理由.
已知函数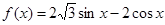
(Ⅰ)若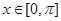 ,求
,求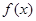 的最大值和最小值;
的最大值和最小值;
(Ⅱ)若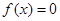 ,求
,求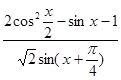 的值.
的值.
已知函数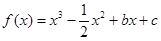 。
。
(Ⅰ)若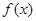 在
在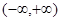 是增函数,求b的取值范围;
是增函数,求b的取值范围;
(Ⅱ)若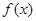 在
在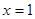 时取得极值,且
时取得极值,且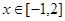 时,
时,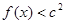 恒成立,求c的取值范围.
恒成立,求c的取值范围.
已知函数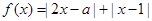 .
.
(Ⅰ)当a = 3时,求不等式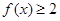 的解集;
的解集;
(Ⅱ)若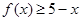 对
对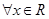 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线 过点P(-2,-4)的直线
过点P(-2,-4)的直线 为参数)与曲线C相交于点M,N两点.
为参数)与曲线C相交于点M,N两点.
(Ⅰ)求曲线C和直线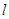 的普通方程;
的普通方程;
(Ⅱ)若|PM|,|MN|,|PN |成等比数列,求实数a的值.
如图,已知 切⊙
切⊙ 于点E,割线PBA交⊙
于点E,割线PBA交⊙ 于A、B两点,∠APE的平分线和AE、BE分别交于点C、D.
于A、B两点,∠APE的平分线和AE、BE分别交于点C、D.
求证:(Ⅰ)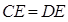 ; (Ⅱ)
; (Ⅱ) .
.