某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:

(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.
如图所示,已知 M、N分别是AC、AD的中点,BC
M、N分别是AC、AD的中点,BC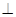 CD.
CD.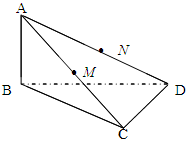
(Ⅰ)求证:MN∥平面BCD;
(Ⅱ)求证:平面B CD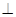 平面ABC;
平面ABC;
(Ⅲ)若AB=1,BC=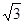 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.
(本小题满分10分)
已知函数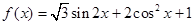
(Ⅰ)求函数 的最小正周期和最小值;
的最小正周期和最小值;
(Ⅱ)设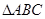 的内角
的内角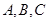 对边分别为
对边分别为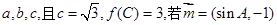 与
与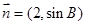 垂直,求
垂直,求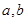 的值.
的值.
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC。
(1)求证:FB=FC;
(2)若AB是△ABC的外接圆的直径,∠EAC =120°,BC=6,求AD的长。
在各项为正的数列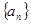 中,数列的前n项和
中,数列的前n项和 满足
满足
(1)求 ;(2) 由(1)猜想数列
;(2) 由(1)猜想数列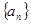 的通项公式;(3) 求
的通项公式;(3) 求
在复平面上,平行四边形ABCD的三个顶点A、B、C 对应的复数分别为 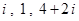 .求第四个顶点D的坐标及此平行四边形的对角线的长.
.求第四个顶点D的坐标及此平行四边形的对角线的长.