(.如图所示,已知四棱锥P—ABCD,底面ABCD为菱形,PA⊥平面ABCD,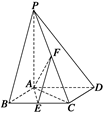
∠ABC=60°,E,F分别是BC,PC的中点.
(1)证明:AE⊥PD;
(2)若H为PD上的动点,EH与平面PAD所成最大角的正切值为 ,
,
求二面角E—AF—C的余弦值.
(满分14分)已知不等式 的解集为A,不等式
的解集为A,不等式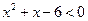 的解集为B。
的解集为B。
(1)求A∩B;
(2)若不等式 的解集为A∩B,求不等式
的解集为A∩B,求不等式 的解集。
的解集。
(满分13分)已知数列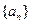 满足
满足 (
(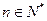 ),它的前
),它的前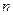 项和为
项和为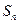 ,且
,且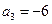 ,
,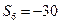 。求数列
。求数列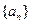 的前
的前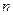 项和的最小值.
项和的最小值.
(满分13分)已知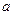 、
、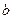 、
、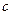 分别是
分别是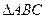 的三个内角
的三个内角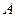 、
、 、
、 所对的边
所对的边
(1)若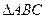 面积
面积 求
求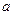 、
、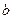 的值;
的值;
(2)若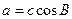 ,且
,且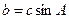 ,试判断
,试判断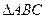 的形状.
的形状.
(本小题满分14分)
(Ⅰ) 已知动点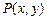 到点
到点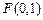 与到直线
与到直线 的距离相等,求点
的距离相等,求点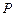 的轨迹
的轨迹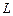 的方程;
的方程;
(Ⅱ) 若正方形 的三个顶点
的三个顶点 ,
, ,
,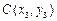 (
(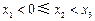 )在(Ⅰ)中的曲线
)在(Ⅰ)中的曲线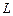 上,设
上,设 的斜率为
的斜率为 ,
,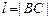 ,求
,求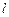 关于
关于 的函数解析式
的函数解析式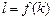 ;
;
(Ⅲ) 求(2)中正方形 面积
面积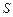 的最小值。
的最小值。
(本小题满分14分)
已知函数 .
.
(Ⅰ)若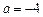 ,求函数
,求函数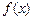 的极值;
的极值;
(Ⅱ)当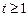 时,不等式
时,不等式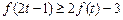 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。