(本小题满分14分)
(Ⅰ) 已知动点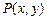 到点
到点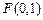 与到直线
与到直线 的距离相等,求点
的距离相等,求点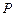 的轨迹
的轨迹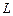 的方程;
的方程;
(Ⅱ) 若正方形 的三个顶点
的三个顶点 ,
, ,
,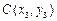 (
(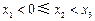 )在(Ⅰ)中的曲线
)在(Ⅰ)中的曲线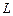 上,设
上,设 的斜率为
的斜率为 ,
,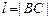 ,求
,求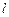 关于
关于 的函数解析式
的函数解析式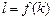 ;
;
(Ⅲ) 求(2)中正方形 面积
面积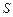 的最小值。
的最小值。
已知二次函数 满足:对任意实数x,都有
满足:对任意实数x,都有 ,且当
,且当 (1,3)时,有
(1,3)时,有 成立。
成立。
(1)证明: ;
;
(2)若 的表达式;
的表达式;
(3)设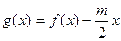 ,
, ,若
,若 图上的点都位于直线
图上的点都位于直线 的上方,求
的上方,求
实数m的取值范围。
已知函数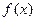 的定义域为R,对任意的
的定义域为R,对任意的 都满足
都满足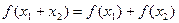 ,当
,当 时,
时,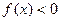 .
.
(1)判断并证明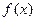 的单调性和奇偶性;
的单调性和奇偶性;
(2)是否存在这样的实数m,当 时,使不等式
时,使不等式
对所有 恒成立,如存在,求出m的取值范围;若不存在,说明理由.
恒成立,如存在,求出m的取值范围;若不存在,说明理由.
已知函数
(Ⅰ)求证:函数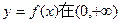 上是增函数.
上是增函数.
(Ⅱ)若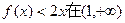 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
(Ⅲ)若函数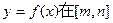 上的值域是
上的值域是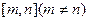 ,求实数a的取值范围.
,求实数a的取值范围.
已知数列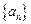 满足
满足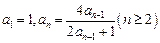 .
.
(1)求数列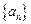 的通项公式;
的通项公式;
(2)证明不等式: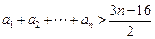 .
.
已知数列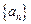 满足
满足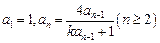 .
.
(1)求数列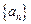 的通项公式;
的通项公式;
(2)当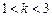 时,证明不等式:
时,证明不等式: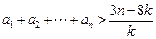 .
.